Space diagonal

AC' (shown in blue) is a space diagonal while AC (shown in red) is a face diagonal

In geometry a space diagonal (or interior diagonal or body diagonal) of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face (but not on the same edge) as each other.^[1]

Axial diagonal

An axial diagonal is a space diagonal that passes through the center of a polyhedron.

For example, in a cube with edge length a, all four space diagonals are axial diagonals, of common length 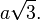$a\sqrt {3}.$ More generally, a cuboid with edge lengths a, b, and c has all four space diagonals axial, with common length $\sqrt{a^2+b^2+c^2}.$

A regular octahedron has 3 axial diagonals, of length $a\sqrt {2}$ , with edge length a.

A regular icosahedron has 6 axial diagonals of length 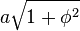$a\sqrt {1+\phi^2}$ , where φ is the golden ratio $(1+\sqrt 5)/2$ .^[2]

Space diagonals of magic cubes

The above picture demonstrates how to graphically build a space diagonal and mathematically calculate it with Pythagoras' Theorem.

For the cube to be considered magic, these four lines must sum correctly.

The word triagonal is derived from the fact that as a variable point travels down the line, three coordinates change. The equivalent in a square is diagonal, because two coordinates change. In a tesseract it is quadragonal because 4 coordinates change, etc.

r-agonals

This section applies particularly to magic hypercubes.

The magic hypercube community has started to recognize an abbreviated expression for these space diagonals. By using r as a variable to describe the various agonals, a concise notation is possible.

If r =

2 then we have a diagonal. 2 coordinates change.
3 = a triagonal. 3 coordinates change
4 = a quadragonal. 4 coordinates change
n = the dimension of the hypercube, the 2^n-1 agonals are required to sum correctly for the hypercube to be considered magic.

... By extension, if r =

1, the line is parallel to a face. Only 1 coordinate changes. A 1-agonal may be called a monagonal, in keeping with a diagonal, a triagonal, etc. Lines parallel to the faces of the hypercube have, in the past, also been referred to as i-rows.

Because the prefix pan indicates all, we can concisely state the characteristics or a magic hypercube.

For example;

If pan-r-agonals sum correctly for r = 1 and 2, we know the square is pandiagonal magic.
If pan-r-agonals sum correctly for r = 1 and 3, we have a pantriagonal magic cube (the equivalent of a pandiagonal magic square).
If the r-agonals sum correctly for r = 1 and n, then the magic hypercube is simple magic regardless of what dimension it is.

The length of an r-agonal of a hypercube with side length a is 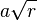$a\sqrt {r}$ .

References

↑ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.116
↑ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865 .

John R. Hendricks, The Pan-3-Agonal Magic Cube, Journal of Recreational Mathematics 5:1:1972, pp 51–54. First published mention of pan-3-agonals
Hendricks, J. R., Magic Squares to Tesseracts by Computer, 1998, 0-9684700-0-9, page 49
Heinz & Hendricks, Magic Square Lexicon: Illustrated, 2000, 0-9687985-0-0, pages 99,165
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 173, 1994.

Space diagonal

Axial diagonal

Space diagonals of magic cubes

r-agonals

See also

References

External links