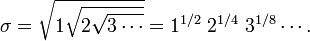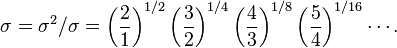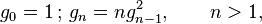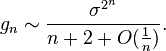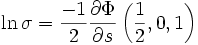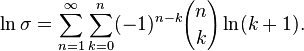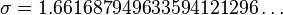Somos' quadratic recurrence constant

In mathematics, Somos' quadratic recurrence constant, named after Michael Somos, is the number

\sigma = \sqrt {1 \sqrt {2 \sqrt{3 \cdots}}} = 1^{1/2}\;2^{1/4}\; 3^{1/8} \cdots.\,

This can be easily re-written into the far more quickly converging product representation

\sigma = \sigma^2/\sigma = \left(\frac{2}{1} \right)^{1/2} \left(\frac{3}{2} \right)^{1/4} \left(\frac{4}{3} \right)^{1/8} \left(\frac{5}{4} \right)^{1/16} \cdots.

The constant σ arises when studying the asymptotic behaviour of the sequence

g_0=1\, ; \, g_n = ng_{n-1}^2, \qquad n > 1, \,

with first few terms 1, 1, 2, 12, 576, 1658880 ... (sequence A052129 in OEIS). This sequence can be shown to have asymptotic behaviour as follows:[1]

g_n \sim \frac {\sigma^{2^n}}{n + 2 + O(\frac{1}{n})}.

Guillera and Sondow give a representation in terms of the derivative of the Lerch transcendent:

\ln \sigma = \frac{-1}{2} \frac {\partial \Phi} {\partial s} \left( \frac{1}{2}, 0, 1 \right)

where ln is the natural logarithm and 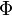\Phi(z, s, q) is the Lerch transcendent.

Using series acceleration it is the sum of the n-th differences of ln(k) at k=1 as given by:

\ln \sigma = \sum_{n=1}^\infty \sum_{k=0}^n (-1)^{n-k} {n \choose k} \ln (k+1).

Finally,

\sigma = 1.661687949633594121296\dots\; (sequence A112302 in OEIS).

Notes

  1. ↑ Weisstein, Eric W., "Somos's Quadratic Recurrence Constant", MathWorld.

References

  • Steven R. Finch, Mathematical Constants (2003), Cambridge University Press, p. 446. ISBN 0-521-81805-2.
  • Jesus Guillera and Jonathan Sondow, "Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent", Ramanujan Journal 16 (2008), 247–270 (Provides an integral and a series representation). arXiv:math/0506319