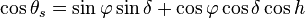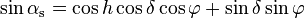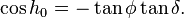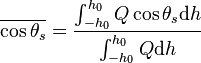Solar zenith angle

The solar zenith angle is the angle measured from directly overhead to the geometric centre of the sun's disc, as described using a horizontal coordinate system. The solar elevation angle is the altitude of the sun, the angle between the horizon and the centre of the sun's disc. If we write θ_s for the solar zenith angle, then the solar elevation angle α_s = 90° – θ_s.^[1]

Formulas

Solar zenith angle

The solar zenith angle, θ_s is estimated using results from spherical trigonometry by^[2]^[3]

\cos \theta_s = \sin \varphi \sin \delta + \cos \varphi \cos \delta \cos h

where

θ_s is the solar zenith angle
h is the hour angle, in the local solar time.
δ is the current declination of the Sun
φ is the local latitude.

Solar elevation angle

The solar elevation angle is the altitude of the sun, the angle between the horizon and the centre of the sun's disc. The approximate value can be calculated with the following formula:

\sin \alpha_\mathrm{s} = \cos h \cos \delta \cos \varphi + \sin \delta \sin \varphi

where

α_s is the solar elevation angle, α_s = 90° – θ_s
h is the hour angle, in the local solar time.
δ is the current declination of the Sun
φ is the local latitude.

Caveats

The values calculated above are approximations due to the distinction between common/geodetic latitude and geocentric latitude. However, the two values differ by less than 12 minutes of arc.

The formulas neglect the effect of atmospheric refraction.

The formula for solar elevation angle was derived using the trigonometric addition formulas from the solar zenith angle formula^[4]

Applications

Sunrise/Sunset

The approximate times of sunset and sunrise occur when the zenith angle is 90°, where the hour angle h₀ satisfies^[3]

\cos h_0 = -\tan \phi \tan \delta.

Precise times of sunset and sunrise occur when the upper limb of the Sun appears, as refracted by the atmosphere, to be on the horizon.

Albedo

A weighted daily average zenith angle, used in computing the local albedo of the Earth, is given by

\overline{\cos \theta_s} = \frac{\int_{-h_0}^{h_0} Q \cos \theta_s \text{d}h}{\int_{-h_0}^{h_0} Q \text{d}h}

where Q is the instantaneous insolation.^[3]

Summary of special angles

For example, the solar elevation angle is :

90° if you are on the equator, a day of equinox, at a solar hour of twelve
near 0° at the sunset or at the sunrise
between -90° and 0° during the night

An exact calculation is given in position of the Sun. Other approximations exist elsewhere.^[5]

References

↑ Schowengerdt, R. A. (2007). "Optical radiation models". Remote Sensing. pp. 45–88. doi:10.1016/B978-012369407-2/50005-X. ISBN 9780123694072.
↑ Jacobson, Mark Z. (2005). Fundamentals of Atmospheric Modeling (2nd ed.). Cambridge University Press. p. 317. ISBN 0521548659.
↑ 3.0 3.1 3.2 Hartmann, Dennis L. (1994). Global Physical Climatology. Academic Press. p. 30. ISBN 0080571638.
↑ Woolf, Harold M. (1968). "On the computation of solar elevation angles and the determination of sunrise and sunset times". NASA technical memorandu, X-1646 (Washington, D.C.): 3.
↑ livioflores-ga. "Equation to know where the Sun is at a given place at a given date-time". Google. Retrieved 9 March 2013.

Solar zenith angle

Formulas