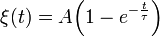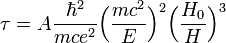Sokolov–Ternov effect
The Sokolov–Ternov effect is the effect of self-polarization of relativistic electrons or positrons moving at high energy in a magnetic field. The self-polarization occurs through the emission of spin-flip synchrotron radiation. The effect was predicted by Igor Ternov which then were rigorously justified by Arseny Sokolov using exact solutions to the Dirac equation.[1][2]
Theory
An electron in a magnetic field can have its spin oriented in the same ("spin up") or in the opposite ("spin down") direction with respect to the direction of the magnetic field (which is assumed to be oriented "up"). The "spin down" state has a higher energy than "spin up" state. The polarization arises due to the fact that the rate of transition through emission of synchrotron radiation to the "spin down" state is slightly greater than the probability of transition to the "spin up" state. As a result, an initially unpolarized beam of high-energy electrons circulating in a storage ring after sufficiently long time will have spins oriented in the direction opposite to the magnetic field. Saturation is not complete and is explicitly described by the formula[3]
where 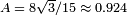 is the limiting degree of polarization (92.4%) and
is the limiting degree of polarization (92.4%) and  is the relaxation time,
is the relaxation time,
Here  is as before,
is as before, 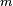 and
and  are the mass and charge of the electron,
are the mass and charge of the electron,  is the speed of light,
is the speed of light, 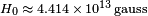 is the Schwinger field,
is the Schwinger field, 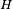 is the magnetic field, and
is the magnetic field, and 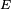 is the electron energy.
is the electron energy.
The limiting degree of polarization  is less than one due to the existence of spin-orbital energy exchange which allows for transitions to the "spin up" state (with probability 25.25 times less than to the "spin down" state).
is less than one due to the existence of spin-orbital energy exchange which allows for transitions to the "spin up" state (with probability 25.25 times less than to the "spin down" state).
Typical relaxation time is on the order of minutes and hours. Thus producing a highly polarized beam requires a long enough time and the use of storage rings.
The self-polarization effect for positrons is similar, with the only difference that positrons will tend to have spins oriented in the direction parallel to the direction of the magnetic field.[4]
Experimental observation
Sokolov–Ternov effect was experimentally observed in the USSR, France, Germany, USA, Japan, and Switzerland in storage rings with electrons of energy 1-50 GeV.[3][5]
- 1971 — Budker Institute of Nuclear Physics (first observation), with the use of 625 MeV storage ring VEPP-2.
- 1971 — Orsay (France), with the use of 536 MeV АСО storage ring.
- 1975 — Stanford (USA), with the use of 2.4 GeV SPEAR storage ring.
- 1980 — DESY, Hamburg (Germany), with the use of 15.2 GeV PETRA.
Applications and generalization
The effect of radiative polarization provides a unique capability for creating polarized beams of high-energy electrons and positrons that can be used for various experiments.
The effect also has been related to the Unruh effect which, up to now, under experimentally achievable conditions is too small to be observed.
The equilibrium polarization given by the Sokolov and Ternov has corrections when the orbit is not perfectly planar. The formula has been generalized by Derbenev and Kondratenko and others.[6]
Patent
- Sokolov A. A. and Ternov I. M. (1973): Award N 131 of 7 August 1973 with priority of 26 June 1963, Byull. Otkr. i Izobr., vol. 47.
See also
Notes
- ↑ Sokolov, A. A.; I. M. Ternov (1963). О поляризационных и спиновых эффектах в теории синхротронного излучения [Polarization and spin effects in the theory of synchrotron radiation]. Doklady Akademii Nauk SSSR (in Russian) 153 (5): 1052–1053.
- ↑ A. A. Sokolov & I. M. Ternov (1964). "On Polarization and Spin Effects in Synchrotron Radiation Theory". Sov. Phys. Dokl. 8: 1203. Bibcode:1964SPhD....8.1203S.
- ↑ 3.0 3.1 A. A. Sokolov & I. M. Ternov (1986). C. W. Kilmister, ed. Radiation from Relativistic Electrons. New York: American Institute of Physics Translation Series. ISBN 0-88318-507-5. Section 21.3 for the theory and section 27.2 for experimental verifications of the Sokolov–Ternov effect.
- ↑ J. Kessler (1985). Polarized Electrons (2nd ed.). Berlin: Springer. Section 6.2.
- ↑ V. A. Bordovitsyn, ed. (1999). Synchrotron Radiation Theory and Its Development: in Memory of I. M. Ternov. Singapore: World Scientific. ISBN 981-02-3156-3.
- ↑ http://pra.aps.org/abstract/PRA/v37/i2/p456_1 "Calculations of Bell and Leinaas and Derbenev and Kondratenko for radiative electron polarization"