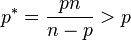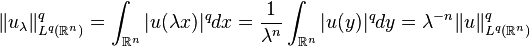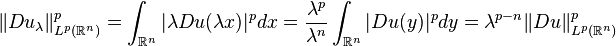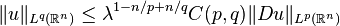Sobolev conjugate

The Sobolev conjugate of p for 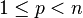1\leq p <n, where n is space dimensionality, is

p^*=\frac{pn}{n-p}>p

This is an important parameter in the Sobolev inequalities.

Motivation

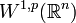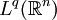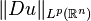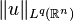A question arises whether u from the Sobolev space W^{1,p}(\mathbb{R}^n) belongs to L^q(\mathbb{R}^n) for some q>p. More specifically, when does \|Du\|_{L^p(\mathbb{R}^n)} control \|u\|_{L^q(\mathbb{R}^n)}? It is easy to check that the following inequality

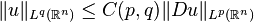\|u\|_{L^q(\mathbb{R}^n)}\leq C(p,q)\|Du\|_{L^p(\mathbb{R}^n)} (*)

can not be true for arbitrary q. Consider 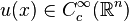u(x)\in C^\infty_c(\mathbb{R}^n), infinitely differentiable function with compact support. Introduce 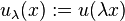u_\lambda(x):=u(\lambda x). We have that

\|u_\lambda\|_{L^q(\mathbb{R}^n)}^q=\int_{\mathbb{R}^n}|u(\lambda x)|^qdx=\frac{1}{\lambda^n}\int_{\mathbb{R}^n}|u(y)|^qdy=\lambda^{-n}\|u\|_{L^q(\mathbb{R}^n)}^q
\|Du_\lambda\|_{L^p(\mathbb{R}^n)}^p=\int_{\mathbb{R}^n}|\lambda Du(\lambda x)|^pdx=\frac{\lambda^p}{\lambda^n}\int_{\mathbb{R}^n}|Du(y)|^pdy=\lambda^{p-n}\|Du\|_{L^p(\mathbb{R}^n)}^p

The inequality (*) for 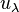u_\lambda results in the following inequality for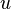 u

\|u\|_{L^q(\mathbb{R}^n)}\leq \lambda^{1-n/p+n/q}C(p,q)\|Du\|_{L^p(\mathbb{R}^n)}

If 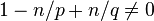1-n/p+n/q\not = 0, then by letting 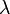\lambda going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for

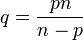q=\frac{pn}{n-p},

which is the Sobolev conjugate.

See also

References