Small snub icosicosidodecahedron
| Small snub icosicosidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 112, E = 180 V = 60 (χ = −8) |
| Faces by sides | (40+60){3}+12{5/2} |
| Wythoff symbol | |5/2 3 3 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U32, C41, W110 |
| Dual polyhedron | Small hexagonal hexecontahedron |
| Vertex figure |  35.5/2 |
| Bowers acronym | Seside |
In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, ß{3,5}.
Convex hull
Its convex hull is a nonuniform truncated icosahedron.
 Truncated icosahedron (regular faces) |
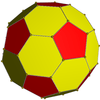 Convex hull (isogonal hexagons) |
 Small snub icosicosidodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a small snub icosicosidodecahedron are all the even permutations of
- (±½(−1/τ+√(3τ−2)), 0, ±½(3+τ√(3τ−2)))
- (±½(1/τ+√(3τ−2)), ±1, ±½(1+2/τ+τ√(3τ−2)))
- (±½(τ2+√(3τ−2)), ±1/τ, ±½(1+τ√(3τ−2)))
where τ = (1+√5)/2 is the golden ratio (sometimes written φ).
See also
External links
- Weisstein, Eric W., "Small snub icosicosidodecahedron", MathWorld.
- Richard Klitzing, 3D star, small snub icosicosidodecahedron