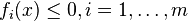Slater's condition

In mathematics, Slater's condition (or Slater condition) is a sufficient condition for strong duality to hold for a convex optimization problem, named after Morton L. Slater.[1] Informally, Slater's condition states that the feasible region must have an interior point (see technical details below).

Slater's condition is a specific example of a constraint qualification. In particular, if Slater's condition holds for the primal problem, then the duality gap is 0, and if the dual value is finite then it is attained.[2]

Details

Given the problem

\text{Minimize }\; f_0(x)
\text{subject to: }\
f_i(x) \le 0 , i = 1,\ldots,m
Ax = b

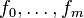with f_0,\ldots,f_m convex (and therefore a convex optimization problem). Then Slater's condition implies that strong duality holds if there exists an 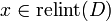x \in \operatorname{relint}(D) (where relint is the relative interior and D = \cap_{i = 0}^m \operatorname{dom}(f_i)) such that

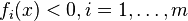f_i(x) < 0, i = 1,\ldots,m and
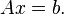Ax = b.\,[3]

If the first 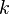k constraints, 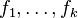f_1,\ldots,f_k are linear functions, then strong duality holds if there exists an 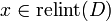x \in \operatorname{relint}(D) such that

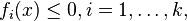
f_i(x) \le 0, i = 1,\ldots,k,
f_i(x) < 0, i = k+1,\ldots,m, and
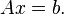Ax = b.\,[3]

Generalized Inequalities

Given the problem

\text{Minimize }\; f_0(x)
\text{subject to: }\
f_i(x) \le_{K_i} 0 , i = 1,\ldots,m
Ax = b

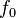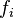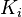where f_0 is convex and f_i is K_i-convex for each 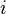i. Then Slater's condition says that if there exists an 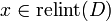x \in \operatorname{relint}(D) such that

f_i(x) <_{K_i} 0, i = 1,\ldots,m and
Ax = b

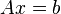
then strong duality holds.[3]

References

  1. ↑ Slater, Morton (1950). Lagrange Multipliers Revisited (Report). Cowles Commission Discussion Paper No. 403.
  2. ↑ Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 978-0-387-29570-1.
  3. ↑ 3.0 3.1 3.2 Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. ISBN 978-0-521-83378-3. Retrieved October 3, 2011.