Slash distribution
|
Probability density function 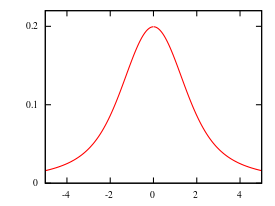 | |
|
Cumulative distribution function  | |
| Parameters | none |
|---|---|
| Support |
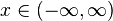 |
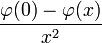 | |
| CDF |
![\begin{cases}
\Phi(x) - \left[ \varphi(0) - \varphi(x) \right] / x & x \ne 0 \\
1 / 2 & x = 0 \\
\end{cases}](../I/m/2d690c7134badfee504cc5ac1ac8d065.png) |
| Mean | Does not exist |
| Median | 0 |
| Mode | 0 |
| Variance | Does not exist |
| Skewness | Does not exist |
| Ex. kurtosis | Does not exist |
| MGF | Does not exist |
| CF |
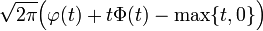 |
In probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate.[1] In other words, if the random variable Z has a normal distribution with zero mean and unit variance, the random variable U has a uniform distribution on [0,1] and Z and U are statistically independent, then the random variable X = Z / U has a slash distribution. The slash distribution is an example of a ratio distribution. The distribution was named by William H. Rogers and John Tukey in a paper published in 1972.[2]
The probability density function (pdf) is
where φ(x) is the probability density function of the standard normal distribution.[3] The result is undefined at x = 0, but the discontinuity is removable:
The most common use of the slash distribution is in simulation studies. It is a useful distribution in this context because it has heavier tails than a normal distribution, but it is not as pathological as the Cauchy distribution.[3]
Differential equation
The pdf of the slash distribution is a solution of the following differential equation:
References
- ↑ Davison, Anthony Christopher; Hinkley, D. V. (1997). Bootstrap methods and their application. Cambridge University Press. p. 484. ISBN 978-0-521-57471-6. Retrieved 24 September 2012.
- ↑ Rogers, W. H.; Tukey, J. W. (1972). "Understanding some long-tailed symmetrical distributions". Statistica Neerlandica 26 (3): 211–226. doi:10.1111/j.1467-9574.1972.tb00191.x.
- ↑ 3.0 3.1 "SLAPDF". Statistical Engineering Division, National Institute of Science and Technology. Retrieved 2009-07-02.
![]() This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.
This article incorporates public domain material from websites or documents of the National Institute of Standards and Technology.
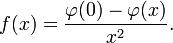
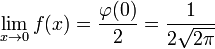
![\left\{\begin{array}{l}
2 \sqrt{\pi} x f'(x)+2 \sqrt{\pi} \left(x^2+2\right) f(x)-\sqrt{2}=0, \\[12pt]
f(1)=\frac{1}{\sqrt{2 \pi}}-\frac{1}{\sqrt{2 e\pi}}
\end{array}\right\}](../I/m/1387c4101782de55a79f1ddee9f98dd5.png)