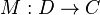Sketch (mathematics)
In the mathematical theory of categories, a sketch is a category D, together with a set of limit cones and a set of colimit cones. A model of the sketch in a category C is a functor
that takes each specified cone to a limit cone in C and each specified cocone to a colimit cocone in C. Morphisms of models are natural transformations. Sketches are a general way of specifying structures on the objects of a category, forming a category-theoretic analog to the logical concept of a theory and its models. They allow multisorted models and models in any category.
Sketches were invented in 1968 by Charles Ehresmann, using a different but equivalent definition. There are still other definitions in the research literature.
References
- Adámek, Jiří; Rosický, Jiří (1994), Locally Presentable and Accessible Categories, London Mathematical Society Lecture Note Series 189, Cambridge: Cambridge University Press, doi:10.1017/CBO9780511600579, ISBN 0-521-42261-2, MR 1294136.
- Barr, Michael; Wells, Charles (2005), Toposes, Triples and Theories, Reprints in Theory and Applications of Categories 12 (revised ed.), MR 2178101.
- Borceux, Francis (1994), Handbook of Categorical Algebra. 2. Categories and Structures, Encyclopedia of Mathematics and its Applications 51, Cambridge: Cambridge University Press, ISBN 0-521-44179-X, MR 1313497.
- Ehresmann, Charles (1968), "Esquisses et types des structures algébriques", Bul. Inst. Politehn. Iaşi (N.S.), 14 (18) (fasc. 1-2): 1–14, MR 0238918.
- Johnstone, Peter T. (2002), Sketches of an elephant: a topos theory compendium. Vol. 2, Oxford Logic Guides 44, Oxford: The Clarendon Press, Oxford University Press, ISBN 0-19-851598-7, MR 2063092.
- Makkai, Michael; Paré, Robert (1989), Accessible Categories: The Foundations of Categorical Model Theory, Contemporary Mathematics 104, Providence, RI: American Mathematical Society, ISBN 0-8218-5111-X, MR 1031717.
External links
- Sketches: Outline with references (updated 2009).
- sketch in nLab