Size homotopy group
The concept of size homotopy group is analogous in size theory of the classical concept of homotopy group. In order to give its definition, let us assume that a size pair 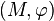 is given, where
is given, where 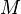 is a closed manifold of class
is a closed manifold of class 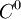 and
and 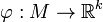 is a continuous function. Let us consider the partial order
is a continuous function. Let us consider the partial order 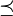 in
in 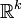 defined by setting
defined by setting 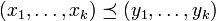 if and only if
if and only if 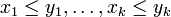 . For every
. For every 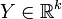 we set
we set 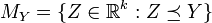 .
.
Assume that 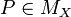 and
and 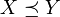 . If
. If 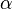 ,
, 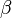 are two paths from
are two paths from 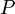 to
to 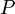 and a homotopy from
and a homotopy from 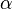 to
to 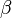 , based at
, based at 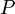 , exists in the topological space
, exists in the topological space 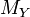 , then we write
, then we write  . The first size homotopy group of the size pair
. The first size homotopy group of the size pair 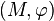 computed at
computed at 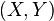 is defined to be the quotient set of the set of all paths from
is defined to be the quotient set of the set of all paths from 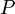 to
to 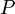 in
in 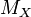 with respect to the equivalence relation
with respect to the equivalence relation 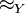 , endowed with the operation induced by the usual composition of based loops.[1]
, endowed with the operation induced by the usual composition of based loops.[1]
In other words, the first size homotopy group of the size pair 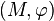 computed at
computed at 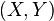 and
and 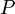 is the image
is the image
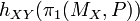 of the first homotopy group
of the first homotopy group 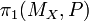 with base point
with base point 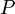 of the topological space
of the topological space 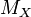 , when
, when 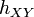 is the homomorphism induced by the inclusion of
is the homomorphism induced by the inclusion of 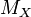 in
in 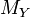 .
.
The 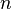 -th size homotopy group is obtained by substituting the loops based at
-th size homotopy group is obtained by substituting the loops based at 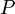 with the continuous functions
with the continuous functions 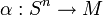 taking a fixed point of
taking a fixed point of 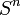 to
to 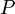 , as happens when higher homotopy groups are defined.
, as happens when higher homotopy groups are defined.
References
- ↑ Patrizio Frosini, Michele Mulazzani, Size homotopy groups for computation of natural size distances, Bulletin of the Belgian Mathematical Society – Simon Stevin, 6:455–464, 1999.