Size functor
Given a size pair  where
where 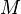 is a manifold of dimension
is a manifold of dimension
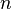 and
and 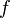 is an arbitrary real continuous function defined
on it, the
is an arbitrary real continuous function defined
on it, the 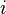 -th size functor,[1] with
-th size functor,[1] with  , denoted
by
, denoted
by  , is the functor in
, is the functor in  , where
, where  is the category of ordered real numbers, and
is the category of ordered real numbers, and  is the category of Abelian groups, defined in the following way. For
is the category of Abelian groups, defined in the following way. For  , setting
, setting  ,
,  ,
,  equal to the inclusion from
equal to the inclusion from  into
into  , and
, and  equal to the morphism in
equal to the morphism in  from
from 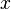 to
to 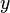 ,
,
- for each
 ,
, 
-

In other words, the size functor studies the
process of the birth and death of homology classes as the lower level set changes.
When 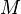 is smooth and compact and
is smooth and compact and 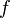 is a Morse function, the functor
is a Morse function, the functor  can be
described by oriented trees, called
can be
described by oriented trees, called  − trees.
− trees.
The concept of size functor was introduced as an extension to homology theory and category theory of the idea of size function. The main motivation for introducing the size functor originated by the observation that the size function  can be seen as the rank
of the image of
can be seen as the rank
of the image of  .
.
The concept of size functor is strictly related to the concept of persistent homology group
,[2]
studied in persistent homology. It is worth to point out that the 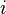 -th persistent homology group coincides with the image of the homomorphism
-th persistent homology group coincides with the image of the homomorphism  .
.
References
- ↑ Francesca Cagliari, Massimo Ferri, Paola Pozzi, Size functions from a categorical viewpoint, Acta Applicandae Mathematicae, 67(3):225-235, 2001.
- ↑ Herbert Edelsbrunner, David Letscher, Afra Zomorodian, Topological Persistence and Simplification, Discrete and Computational Geometry, 28(4):511-533, 2002.