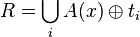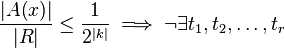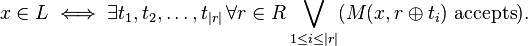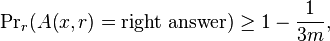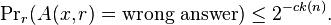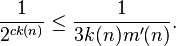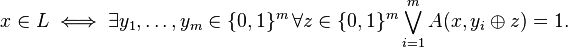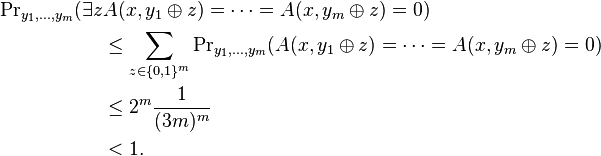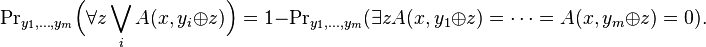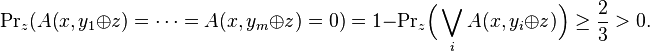Sipser–Lautemann theorem
In computational complexity theory, the Sipser–Lautemann theorem or Sipser–Gács–Lautemann theorem states that Bounded-error Probabilistic Polynomial (BPP) time, is contained in the polynomial time hierarchy, and more specifically Σ2 ∩ Π2.
In 1983, Michael Sipser showed that BPP is contained in the polynomial time hierarchy.[1] Péter Gács showed that BPP is actually contained in Σ2 ∩ Π2. Clemens Lautemann contributed by giving a simple proof of BPP’s membership in Σ2 ∩ Π2, also in 1983.[2] It is conjectured that in fact BPP=P, which is a much stronger statement than the Sipser–Lautemann theorem.
Proof
Here we present the Lautemann's proof,[2] distinguishing the parts that are about containment in polynomial hierarchy and containment in Σ2.
BPP containment in polynomial hierarchy
This part is what Michael Sipser first proved.[1] Without loss of generality, a machine M ∈ BPP with error ≤ 2-|x| can be chosen. (All BPP problems can be amplified to reduce the error probability exponentially.) The basic idea of the proof is to define a Σ2 ∩ Π2 sentence that is equivalent to stating that x is in the language, L, defined by M by using a set of transforms of the random variable inputs.
Since the output of M depends on random input, as well as the input x, it is useful to define which random strings produce the correct output as A(x) = {r | M(x,r) accepts}. The key to the proof is to note that when x ∈ L, A(x) is very large and when x ∉ L, A(x) is very small. By using bitwise parity, ⊕, a set of transforms can be defined as A(x) ⊕ t={r ⊕ t | r ∈ A(x)}. The first main lemma of the proof shows that the union of a small finite number of these transforms will contain the entire space of random input strings. Using this fact, a Σ2 sentence and a Π2 sentence can be generated that is true if and only if x ∈ L (see corollary).
Lemma 1
The general idea of lemma one is to prove that if A(x) covers a large part of the random space 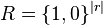 then there exists a small set of translations that will cover the entire random space. In more mathematical language:
then there exists a small set of translations that will cover the entire random space. In more mathematical language:
- If
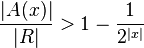 , then
, then 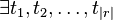 , where
, where 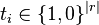 such that
such that 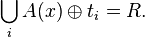
Proof. Randomly pick t1, t2, ..., t|r|. Let 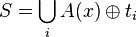 (the union of all transforms of A(x)).
(the union of all transforms of A(x)).
So, for all r in R,
The probability that there will exist at least one element in R not in S is
Therefore
Thus there is a selection for each 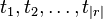 such that
such that
Lemma 2
The previous lemma shows that A(x) can cover every possible point in the space using a small set of translations. Complementary to this, for x ∉ L only a small fraction of the space is covered by A(x). Therefore the set of random strings causing M(x,r) to accept cannot be generated by a small set of vectors ti.
R is the set of all accepting random strings, exclusive-or'd with vectors ti.
Corollary
An important corollary of the lemmas shows that the result of the proof can be expressed as a Σ2 expression, as follows.
That is, x is in language L if and only if there exist |r| binary vectors, where for all random bit vectors r, TM M accepts at least one random vector ⊕ ti.
The above expression is in Σ2 in that it is first existentially then universally quantified. Therefore BPP ⊆ Σ2. Because BPP is closed under complement, this proves BPP ⊆ Σ2 ∩ Π2
BPP containment in Σ2
This part is Laudemann's contribution to the theorem.
Lemma 3
Based on the definition of BPP we show the following:
If L is in BPP then there is an algorithm A such that for every x,
where m is the number of random bits 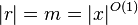 and A runs in time
and A runs in time 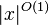 .
.
Proof: Let A ' be a BPP algorithm for L. For every x, 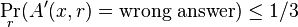 . A ' uses m '(n) random bits where n = |x|.
Do k(n) repetitions of A ' and accept if and only if at least k(n)/2 executions of A ' accept. Define this new algorithm as A. So A uses k(n)m '(n) random bits and
. A ' uses m '(n) random bits where n = |x|.
Do k(n) repetitions of A ' and accept if and only if at least k(n)/2 executions of A ' accept. Define this new algorithm as A. So A uses k(n)m '(n) random bits and
We can then find k(n) with 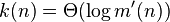 such that
such that
Theorem 1
Proof: Let L be in BPP and A as in Lemma 3. We want to show
where m is the number of random bits used by A on input x. Given  , then
, then
Thus
Thus 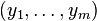 exists.
exists.
Conversely, suppose 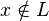 . Then
. Then
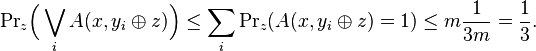
Thus
Thus there is a z such that 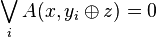 for all
for all 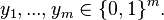
Stronger version
The theorem can be strengthened to 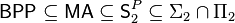 (see MA, SP
(see MA, SP
2).
References
- ↑ 1.0 1.1 Sipser, Michael (1983). "A complexity theoretic approach to randomness". Proceedings of the 15th ACM Symposium on Theory of Computing (ACM Press): 330–335.
- ↑ 2.0 2.1 Lautemann, Clemens (1983). "BPP and the polynomial hierarchy". Inf. Proc. Lett. 17 (4): 215–217.
![\Pr [r \notin S] = \Pr [r \notin A(x) \oplus t_1] \cdot \Pr [r \notin A(x) \oplus t_2] \cdots \Pr [r \notin A(x) \oplus t_{|r|}] \le { \frac{1}{2^{|x| \cdot |r|}} }.](../I/m/f83e6e57ac81107fb7a6ad6fec01ee0b.png)
![\Pr \Bigl[ \bigvee_i (r_i \notin S)\Bigr] \le \sum_i \frac{1}{2^{|x| \cdot |r|}} = \frac{1}{2^{|x|}} < 1.](../I/m/a68a3be2a62ba82ebe7b84a269464aa2.png)
![\Pr [S = R] \ge 1 - \frac{1}{2^{|x|}}.](../I/m/6176080109ea1b8713704d7bdfec7d1a.png)