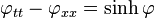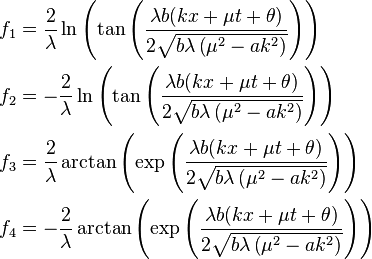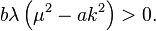Sinh-Gordon

The sinh-Gordon equation is a nonlinear partial differential equation^[1]

\varphi_{tt}- \varphi_{xx} = \sinh\varphi

that has applications in physics and hydrodynamics. It is known for its soliton solutions and arises as a special case of the Toda lattice equation.^[2]

Exact solutions

\begin{align} f_1 &= \frac{2}{\lambda}\ln\left(\tan\left(\frac{\lambda b(kx+\mu t+\theta)}{2\sqrt{b\lambda \left (\mu^2-ak^2 \right )}}\right)\right) \\ f_2 &= -\frac{2}{\lambda}\ln\left(\tan\left(\frac{\lambda b(kx+\mu t+\theta)}{2\sqrt{b\lambda \left (\mu^2-ak^2 \right )}}\right)\right) \\ f_3 &= \frac{2}{\lambda}\arctan\left(\exp\left(\frac{\lambda b(kx+\mu t+\theta)}{2\sqrt{b\lambda \left (\mu^2-ak^2 \right )}}\right)\right) \\ f_4 &= -\frac{2}{\lambda}\arctan\left(\exp\left(\frac{\lambda b(kx+\mu t+\theta)}{2\sqrt{b\lambda \left (\mu^2-ak^2 \right )}}\right)\right) \end{align}

where $k, μ$ , and $θ$ are arbitrary constants and it is assumed that

b\lambda \left (\mu^2-ak^2 \right )>0.

Gallery

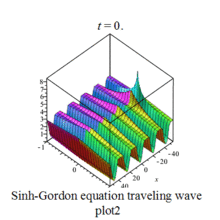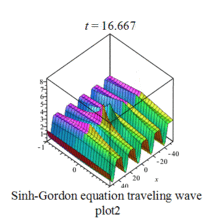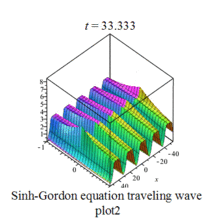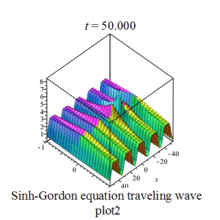Sinh-Gordon eq plot

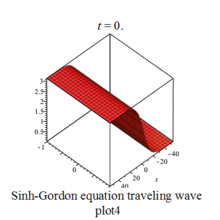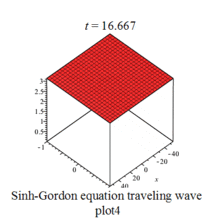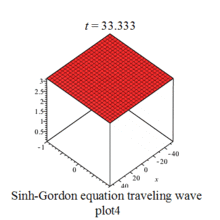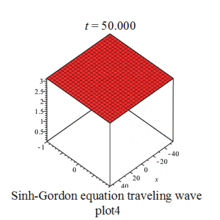Sinh-Gordon eq plot

Sinh-Gordon eq plot

Sinh-Gordon eq plot

References

↑ Andrei D. Polyanin,Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION p485 CRC PRESS
↑ Yuanxi, Xie; Tang, Jiashi (February 2006). Il Nuovo Cimento B 121 (2): 115–121. doi:10.1393/ncb/i2005-10164-6. Missing or empty |title= (help)