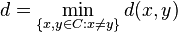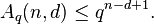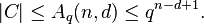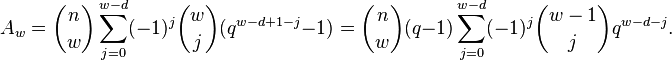Singleton bound
In coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of an arbitrary block code  with block length
with block length  , size
, size  and minimum distance
and minimum distance  .
.
Statement of the bound
The minimum distance of a set  of codewords of length
of codewords of length  is defined as
is defined as
where 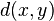 is the Hamming distance between
is the Hamming distance between  and
and  . The expression
. The expression 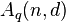 represents the maximum number of possible codewords in a q-ary block code of length
represents the maximum number of possible codewords in a q-ary block code of length  and minimum distance
and minimum distance  .
.
Then the Singleton bound states that
Proof
First observe that the number of  -ary words of length
-ary words of length  is
is 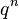 , since each letter in such a word may take one of
, since each letter in such a word may take one of  different values, independently of the remaining letters.
different values, independently of the remaining letters.
Now let  be an arbitrary q-ary block code of minimum distance
be an arbitrary q-ary block code of minimum distance  . Clearly, all codewords
. Clearly, all codewords 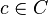 are distinct. If we puncture the code by deleting the first
are distinct. If we puncture the code by deleting the first 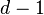 letters of each codeword, then all resulting codewords must still be pairwise different, since all of the original codewords in
letters of each codeword, then all resulting codewords must still be pairwise different, since all of the original codewords in  have Hamming distance at least
have Hamming distance at least  from each other. Thus the size of the altered code is the same as the original code.
from each other. Thus the size of the altered code is the same as the original code.
The newly obtained codewords each have length
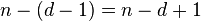 ,
,
and thus, there can be at most 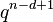 of them. Since
of them. Since  was arbitrary, this bound must hold for the largest possible code with these parameters, thus:[1]
was arbitrary, this bound must hold for the largest possible code with these parameters, thus:[1]
Linear codes
If  is a linear code with block length
is a linear code with block length  , dimension
, dimension  and minimum distance
and minimum distance  over the finite field with
over the finite field with  elements, then the maximum number of codewords is
elements, then the maximum number of codewords is 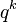 and the Singleton bound implies:
and the Singleton bound implies:
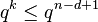 ,
,
so that
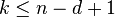 ,
,
which is usually written as[2]
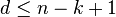 .
.
In the linear code case a different proof of the Singleton bound can be obtained by observing that rank of the parity check matrix is 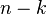 .[3]
.[3]
History
The usual citation given for this result is Singleton (1964), but according to Welsh (1988, p. 72) the result can be found in a 1953 paper of Komamiya.[4]
MDS codes
Linear block codes that achieve equality in the Singleton bound are called MDS (maximum distance separable) codes. Examples of such codes include codes that have only two codewords (the all-zero word and the all-one word, having thus minimum distance n), codes that use the whole of 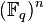 (minimum distance 1), codes with a single parity symbol (minimum distance 2) and their dual codes. These are often called trivial MDS codes.
(minimum distance 1), codes with a single parity symbol (minimum distance 2) and their dual codes. These are often called trivial MDS codes.
In the case of binary alphabets, only trivial MDS codes exist.[5][6]
Examples of non-trivial MDS codes include Reed-Solomon codes and their extended versions.[7][8] In fact, it was proved by Simeon Ball that the only linear q-ary [n,k,d] MDS codes, for k < p+1, where p is the characteristic of the finite field, are given by the Reed-Solomon codes.[9]
MDS codes are an important class of block codes since, for a fixed  and
and  , they have the greatest error correcting and detecting capabilities. There are several ways to characterize MDS codes:[10]
, they have the greatest error correcting and detecting capabilities. There are several ways to characterize MDS codes:[10]
Theorem: Let  be a linear [
be a linear [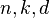 ] code over
] code over 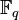 . The following are equivalent:
. The following are equivalent:
-
 is an MDS code.
is an MDS code. - Any
 columns of a generator matrix for
columns of a generator matrix for  are linearly independent.
are linearly independent. - Any
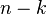 columns of a parity check matrix for
columns of a parity check matrix for  are linearly independent.
are linearly independent. -
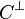 is an MDS code.
is an MDS code. - If
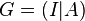 is a generator matrix for
is a generator matrix for  in standard form, then every square submatrix of
in standard form, then every square submatrix of  is nonsingular.
is nonsingular. - Given any
 coordinate positions, there is a (minimum weight) codeword whose support is precisely these positions.
coordinate positions, there is a (minimum weight) codeword whose support is precisely these positions.
The last of these characterizations permits, by using the MacWilliams identities, an explicit formula for the complete weight distribution of an MDS code.[11]
Theorem: Let  be a linear [
be a linear [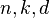 ] MDS code over
] MDS code over 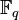 . If
. If 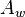 denotes the number of codewords in
denotes the number of codewords in  of weight
of weight 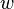 , then
, then
Arcs in projective geometry
The linear independence of the columns of a generator matrix of an MDS code permits a construction of MDS codes from objects in finite projective geometry. Let 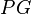 (
(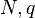 ) be the finite projective space of (geometric) dimension
) be the finite projective space of (geometric) dimension  over the finite field
over the finite field 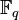 . Let
. Let 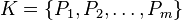 be a set of points in this projective space represented with homogeneous coordinates. Form the
be a set of points in this projective space represented with homogeneous coordinates. Form the 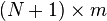 matrix
matrix  whose columns are the homogeneous coordinates of these points. Then,[12]
whose columns are the homogeneous coordinates of these points. Then,[12]
Theorem:  is a (spacial) m-arc if and only if
is a (spacial) m-arc if and only if  is the generator matrix of an [
is the generator matrix of an [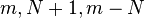 ] MDS code over
] MDS code over 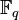 .
.
See also
Notes
- ↑ Ling & Xing 2004, p. 93
- ↑ Roman 1992, p. 175
- ↑ Pless 1998, p. 26
- ↑ Komamiya, Y. (1953), "Application of logical mathematics to information theory", Proc. 3rd Japan. Nat. Cong. Appl. Math.: 437
- ↑ Vermani 1996, Proposition 9.2
- ↑ Ling & Xing 2004, p. 94 Remark 5.4.7
- ↑ MacWilliams & Sloane 1977, Ch. 11
- ↑ Ling & Xing 2004, p. 94
- ↑ Ball, Simeon (2012), "On sets of vectors of a finite vector space in which every subset of basis size is a basis", Journal of the European Mathematical Society 14: 733–748
- ↑ Roman 1992, p. 237, Theorem 5.3.7
- ↑ Roman 1992, p. 240
- ↑ Bruen, A.A.; Thas, J.A.; Blokhuis, A. (1988), "On M.D.S. codes, arcs in PG(n,q), with q even, and a solution of three fundamental problems of B. Segre", Invent. Math. 92: 441–459, doi:10.1007/bf01393742
References
- Ling, San; Xing, Chaoping (2004), Coding Theory / A First Course, Cambridge University Press, ISBN 0-521-52923-9
- MacWilliams, F.J.; Sloane, N.J.A. (1977), The Theory of Error-Correcting Codes, North-Holland, pp. 33, 37, ISBN 0-444-85193-3
- Pless, Vera (1998), Introduction to the Theory of Error-Correcting Codes (3rd ed.), Wiley Interscience, ISBN 0-471-19047-0
- Roman, Steven (1992), Coding and Information Theory, GTM 134, Springer-Verlag, ISBN 0-387-97812-7
- Singleton, R.C. (1964), "Maximum distance q-nary codes", IEEE Trans. Inf. Theory 10 (2): 116–118, doi:10.1109/TIT.1964.1053661
- Vermani, L. R. (1996), Elements of algebraic coding theory, Chapman & Hall
- Welsh, Dominic (1988), Codes and Cryptography, Oxford University Press, ISBN 0-19-853287-3
Further reading
- J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed.). Springer-Verlag. p. 61. ISBN 3-540-54894-7.
- Niederreiter, Harald; Xing, Chaoping (2001). "6. Applications to algebraic coding theory". Rational points on curves over finite fields. Theory and Applications. London Mathematical Society Lecture Note Series 285. Cambridge: Cambridge University Press. ISBN 0-521-66543-4. Zbl 0971.11033.