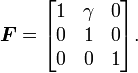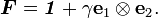Simple shear

In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:

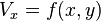
\ V_x=f(x,y)

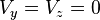
\ V_y=V_z=0

And the gradient of velocity is constant and perpendicular to the velocity itself:

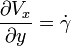\frac {\partial V_x} {\partial y} = \dot \gamma ,

where 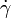\dot \gamma is the shear rate and:

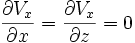
\frac {\partial V_x} {\partial x} = \frac {\partial V_x} {\partial z} = 0

The deformation gradient tensor 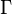\Gamma for this deformation has only one non-zero term:

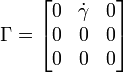
\Gamma = \begin{bmatrix} 0 & {\dot \gamma} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}

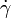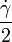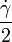Simple shear with the rate \dot \gamma is the combination of pure shear strain with the rate of \dot \gamma \over 2 and rotation with the rate of \dot \gamma \over 2:

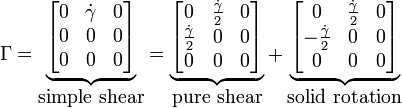
\Gamma = \begin{matrix} \underbrace \begin{bmatrix} 0 & {\dot \gamma} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ \mbox{simple shear}\end{matrix} = \begin{matrix} \underbrace \begin{bmatrix} 0 & {\dot \gamma \over 2} & 0 \\ {\dot \gamma \over 2} & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ \mbox{pure shear} \end{matrix} + \begin{matrix} \underbrace \begin{bmatrix} 0 & {\dot \gamma \over 2} & 0 \\ {- { \dot \gamma \over 2}} & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \\ \mbox{solid rotation} \end{matrix}

Important examples of simple shear include laminar flow through long channels of constant cross-section (Poiseuille flow), and elastomeric bearing pads in base isolation systems to allow critical buildings to survive earthquakes undamaged.

Simple shear in solid mechanics

In solid mechanics, a simple shear deformation is defined as an isochoric plane deformation in which there are a set of line elements with a given reference orientation that do not change length and orientation during the deformation.[1] This deformation is differentiated from a pure shear by virtue of the presence of a rigid rotation of the material.[2][3]

If 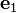\mathbf{e}_1 is the fixed reference orientation in which line elements do not deform during the deformation and 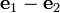\mathbf{e}_1-\mathbf{e}_2 is the plane of deformation, then the deformation gradient in simple shear can be expressed as

\boldsymbol{F} = \begin{bmatrix} 1 & \gamma & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}.

We can also write the deformation gradient as

\boldsymbol{F} = \boldsymbol{\mathit{1}} + \gamma\mathbf{e}_1\otimes\mathbf{e}_2.

See also

References

  1. ↑ Ogden, R. W., 1984, Non-linear elastic deformations, Dover.
  2. ↑ "Where do the Pure and Shear come from in the Pure Shear test?". Retrieved 12 April 2013.
  3. ↑ "Comparing Simple Shear and Pure Shear". Retrieved 12 April 2013.