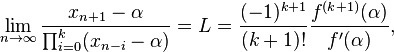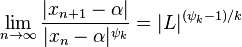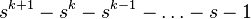Sidi's generalized secant method
Sidi's generalized secant method is a root-finding algorithm, that is, a numerical method for solving equations of the form 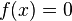 . The method was published
by Avram Sidi.[1]
. The method was published
by Avram Sidi.[1]
The method is a generalization of the secant method. Like the secant method, it is an iterative method which requires one evaluation of  in each iteration and no derivatives of
in each iteration and no derivatives of  . The method can converge much faster though, with an order which approaches 2 provided that
. The method can converge much faster though, with an order which approaches 2 provided that  satisfies the regularity conditions described below.
satisfies the regularity conditions described below.
Algorithm
We call  the root of
the root of  , that is,
, that is, 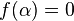 . Sidi's method is an iterative method which generates a sequence
. Sidi's method is an iterative method which generates a sequence 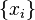 of approximations of
of approximations of  . Starting with k + 1 initial approximations
. Starting with k + 1 initial approximations 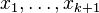 , the approximation
, the approximation 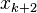 is calculated in the first iteration, the approximation
is calculated in the first iteration, the approximation 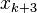 is calculated in the second iteration, etc. Each iteration takes as input the last k + 1 approximations and the value of
is calculated in the second iteration, etc. Each iteration takes as input the last k + 1 approximations and the value of  at those approximations. Hence the nth iteration takes as input the approximations
at those approximations. Hence the nth iteration takes as input the approximations 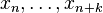 and the values
and the values 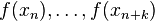 .
.
The number k must be 1 or larger: k = 1, 2, 3, .... It remains fixed during the execution of the algorithm. In order to obtain the starting approximations 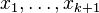 one could carry out a few initializing iterations with a lower value of k.
one could carry out a few initializing iterations with a lower value of k.
The approximation 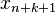 is calculated as follows in the nth iteration. A polynomial of interpolation
is calculated as follows in the nth iteration. A polynomial of interpolation 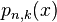 of degree k is fitted to the k + 1 points
of degree k is fitted to the k + 1 points 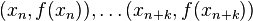 . With this polynomial, the next approximation
. With this polynomial, the next approximation 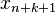 of
of  is calculated as
is calculated as
-
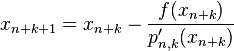
(1)
with 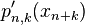 the derivative of
the derivative of 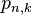 at
at 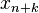 . Having calculated
. Having calculated 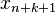 one calculates
one calculates 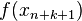 and the algorithm can continue with the (n + 1)th iteration. Clearly, this method requires the function
and the algorithm can continue with the (n + 1)th iteration. Clearly, this method requires the function  to be evaluated only once per iteration; it requires no derivatives of
to be evaluated only once per iteration; it requires no derivatives of  .
.
The iterative cycle is stopped if an appropriate stop-criterion is met. Typically the criterion is that the last calculated approximation is close enough to the sought-after root  .
.
To execute the algorithm effectively, Sidi's method calculates the interpolating polynomial 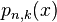 in its Newton form.
in its Newton form.
Convergence
Sidi showed that if the function  is (k + 1)-times continuously differentiable in an open interval
is (k + 1)-times continuously differentiable in an open interval 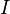 containing
containing  (that is,
(that is, 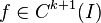 ),
),  is a simple root of
is a simple root of  (that is,
(that is, 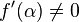 ) and the initial approximations
) and the initial approximations 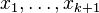 are chosen close enough to
are chosen close enough to  , then the sequence
, then the sequence 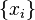 converges to
converges to  , meaning that the following limit holds:
, meaning that the following limit holds: 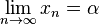 .
.
Sidi furthermore showed that
and that the sequence converges to  of order
of order 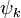 , i.e.
, i.e.
The order of convergence 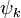 is the only positive root of the polynomial
is the only positive root of the polynomial
We have e.g. 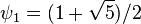 ≈ 1.6180,
≈ 1.6180, 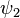 ≈ 1.8393 and
≈ 1.8393 and 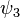 ≈ 1.9276. The order approaches 2 from below if k becomes large:
≈ 1.9276. The order approaches 2 from below if k becomes large: 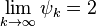 [2]
[3]
[2]
[3]
Related algorithms
Sidi's method reduces to the secant method if we take k = 1. In this case the polynomial 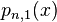 is the linear approximation of
is the linear approximation of  around
around  which is used in the nth iteration of the secant method.
which is used in the nth iteration of the secant method.
We can expect that the larger we choose k, the better 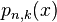 is an approximation of
is an approximation of 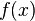 around
around 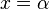 . Also, the better
. Also, the better 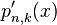 is an approximation of
is an approximation of  around
around 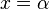 . If we replace
. If we replace 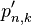 with
with 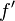 in (1) we obtain that the next approximation in each iteration is calculated as
in (1) we obtain that the next approximation in each iteration is calculated as
-
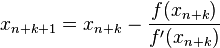
(2)
This is the Newton–Raphson method. It starts off with a single approximation  so we can take k = 0 in (2). It does not require an interpolating polynomial but instead one has to evaluate the derivative
so we can take k = 0 in (2). It does not require an interpolating polynomial but instead one has to evaluate the derivative 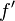 in each iteration. Depending on the nature of
in each iteration. Depending on the nature of  this may not be possible or practical.
this may not be possible or practical.
Once the interpolating polynomial 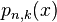 has been calculated, one can also calculate the next approximation
has been calculated, one can also calculate the next approximation 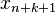 as a solution of
as a solution of 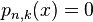 instead of using (1). For k = 1 these two methods are identical: it is the secant method. For k = 2 this method is known as Muller's method.[3] For k = 3 this approach involves finding the roots of a cubic function, which is unattractively complicated. This problem becomes worse for even larger values of k. An additional complication is that the equation
instead of using (1). For k = 1 these two methods are identical: it is the secant method. For k = 2 this method is known as Muller's method.[3] For k = 3 this approach involves finding the roots of a cubic function, which is unattractively complicated. This problem becomes worse for even larger values of k. An additional complication is that the equation 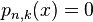 will in general have multiple solutions and a prescription has to be given which of these solutions is the next approximation
will in general have multiple solutions and a prescription has to be given which of these solutions is the next approximation 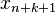 . Muller does this for the case k = 2 but no such prescriptions appear to exist for k > 2.
. Muller does this for the case k = 2 but no such prescriptions appear to exist for k > 2.
References
- ↑ Sidi, Avram, "Generalization Of The Secant Method For Nonlinear Equations", Applied Mathematics E-notes 8 (2008), 115–123, http://www.math.nthu.edu.tw/~amen/2008/070227-1.pdf
- ↑ Traub, J.F., "Iterative Methods for the Solution of Equations", Prentice Hall, Englewood Cliffs, N.J. (1964)
- ↑ 3.0 3.1 Muller, David E., "A Method for Solving Algebraic Equations Using an Automatic Computer", Mathematical Tables and Other Aids to Computation 10 (1956), 208–215