Short supermultiplet

In theoretical physics, a short supermultiplet is a supermultiplet i.e. a representation of the supersymmetry algebra whose dimension is smaller than 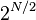where is the number of real supercharges. The representations that saturate the bound are known as the long supermultiplets.

The states in a long supermultiplet may be produced from a representative by the action of the lowering and raising operators, assuming that for any basis vector, either the lowering operator or its conjugate raising operator produce a new nonzero state. This is the reason for the dimension indicated above. On the other hand, the short supermultiplets admit a subset of supercharges that annihilate the whole representation. That is why the short supermultiplets contain the BPS states, another description of the same concept.

The BPS states are only possible for objects that are either massless or massive extremal, i.e. carrying a maximum allowed value of some central charges.