Shock wave

A shock wave is a type of propagating disturbance. When a wave moves faster than the speed of sound in a liquid, gas or plasma (a "fluid", in physics terminology) it is a shock wave. Like an ordinary wave, a shock wave carries energy, and can propagate through a medium. It is characterized by an abrupt, nearly discontinuous change in pressure, temperature and density of the medium.[1] In supersonic flows, expansion is achieved through an expansion fan.
Unlike solitons (another kind of nonlinear wave), the energy of a shock wave dissipates relatively quickly with distance. Also, the accompanying expansion wave approaches and eventually merges with the shock wave, partially cancelling it out. Thus the sonic boom associated with the passage of a supersonic aircraft is the sound wave resulting from the degradation and merging of the shock wave and the expansion wave produced by the aircraft.
When a shock wave passes through matter, the total energy is preserved but the energy which can be extracted as work decreases and the entropy increases. This, for example, creates additional drag force on aircraft with shocks.
Shock waves can travel through any medium, including solids, liquids, gasses, and plasmas.
Terminology
Shock waves can be:
- Normal: at 90° (perpendicular) to the shock medium's flow direction.
- Oblique: at an angle to the direction of flow.
- Bow: Occurs upstream of the front (bow) of a blunt object when the upstream flow velocity exceeds Mach 1.
Some other terms
- Shock Front: an alternative name for the shock wave itself
- Contact Front: in a shock wave caused by a driver gas (for example the "impact" of a high explosive on the surrounding air), the boundary between the driver (explosive products) and the driven (air) gases. The Contact Front trails the Shock Front.
In supersonic flows

The abruptness of change in the features of the medium, that characterize shock waves, can be viewed as a phase transition: the pressure-time diagram of a supersonic object propagating shows how the transition induced by a shock wave is analogous to a dynamic phase transition.
When an object (or disturbance) moves faster than the information about it can be propagated into the surrounding fluid, fluid near the disturbance cannot react or "get out of the way" before the disturbance arrives. In a shock wave the properties of the fluid (density, pressure, temperature, flow velocity, Mach number) change almost instantaneously. Measurements of the thickness of shock waves in air have resulted in values around 200 nm (about 10−5 in),[2] which is on the same order of magnitude as the mean free gas molecule path. In reference to the continuum, this implies the shock wave can be treated as either a line or a plane if the flow field is two-dimensional or three-dimensional, respectively.
Shock waves form when the speed of a fluid changes by more than the speed of sound.[3] At the region where this occurs, sound waves travelling against the flow reach a point where they cannot travel any further upstream and the pressure progressively builds in that region; a high pressure shock wave rapidly forms.
Shock waves are not conventional sound waves; a shock wave takes the form of a very sharp change in the gas properties. Shock waves in air are heard as a loud "crack" or "snap" noise. Over longer distances, a shock wave can change from a nonlinear wave into a linear wave, degenerating into a conventional sound wave as it heats the air and loses energy. The sound wave is heard as the familiar "thud" or "thump" of a sonic boom, commonly created by the supersonic flight of aircraft.
The shock wave is one of several different ways in which a gas in a supersonic flow can be compressed. Some other methods are isentropic compressions, including Prandtl-Meyer compressions. The method of compression of a gas results in different temperatures and densities for a given pressure ratio which can be analytically calculated for a non-reacting gas. A shock wave compression results in a loss of total pressure, meaning that it is a less efficient method of compressing gases for some purposes, for instance in the intake of a scramjet. The appearance of pressure-drag on supersonic aircraft is mostly due to the effect of shock compression on the flow.
Normal shocks
In elementary fluid mechanics utilizing ideal gases, a shock wave is treated as a discontinuity where entropy increases over a nearly infinitesimal region. Since no fluid flow is discontinuous, a control volume is established around the shock wave, with the control surfaces that bound this volume parallel to the shock wave (with one surface on the pre-shock side of the fluid medium and one on the post-shock side). The two surfaces are separated by a very small depth such that the shock itself is entirely contained between them. At such control surfaces, momentum, mass flux and energy are constant; within combustion, detonations can be modelled as heat introduction across a shock wave. It is assumed the system is adiabatic (no heat exits or enters the system) and no work is being done. The Rankine–Hugoniot conditions arise from these considerations.
Taking into account the established assumptions, in a system where the downstream properties are becoming subsonic: the upstream and downstream flow properties of the fluid are considered isentropic. Since the total amount of energy within the system is constant, the stagnation enthalpy remains constant over both regions. Though, entropy is increasing; this must be accounted for by a drop in stagnation pressure of the downstream fluid.
Other shocks
Oblique shocks
When analyzing shock waves in a flow field, which are still attached to the body, the shock wave which is deviating at some arbitrary angle from the flow direction is termed oblique shock. These shocks require a component vector analysis of the flow; doing so allows for the treatment of the flow in an orthogonal direction to the oblique shock as a normal shock.
Bow shocks
When an oblique shock is likely to form at an angle which can not remain on the surface, a nonlinear phenomenon arises where the shock wave will form a continuous pattern around the body. These are termed bow shocks. In these cases, the 1d flow model is not valid and a complex analysis is needed to predict the pressure forces which are exerted on the surface.
Due to nonlinear steepening
Shock waves can form due to steepening of ordinary waves. The best-known example of this phenomenon is ocean waves that form breakers on the shore. In shallow water, the speed of surface waves is dependent on the depth of the water. An incoming ocean wave has a slightly higher wave speed near the crest of each wave than near the troughs between waves, because the wave height is not infinitesimal compared to the depth of the water. The crests overtake the troughs until the leading edge of the wave forms a vertical face and spills over to form a turbulent shock (a breaker) that dissipates the wave's energy as sound and heat.
Similar phenomena affect strong sound waves in gas or plasma, due to the dependence of the sound speed on temperature and pressure. Strong waves heat the medium near each pressure front, due to adiabatic compression of the air itself, so that high pressure fronts outrun the corresponding pressure troughs. While shock formation by this process does not normally happen to sound waves in Earth's atmosphere, it is thought to be one mechanism by which the solar chromosphere and corona are heated, via waves that propagate up from the solar interior.
Analogies
A shock wave may be described as the furthest point upstream of a moving object which "knows" about the approach of the object. In this description, the shock wave position is defined as the boundary between the zone having no information about the shock-driving event and the zone aware of the shock-driving event, analogous with the light cone described in the theory of special relativity.
To produce a shock wave, an object in a given medium (such as air or water) must travel faster than the local speed of sound. In the case of an aircraft travelling at high subsonic speed, regions of air around the aircraft may be travelling at exactly the speed of sound, so that the sound waves leaving the aircraft pile up on one another, similar to a traffic jam on a motorway. When a shock wave forms, the local air pressure increases and then spreads out sideways. Because of this amplification effect, a shock wave can be very intense, more like an explosion when heard at a distance (not coincidentally, since explosions create shock waves).
Analogous phenomena are known outside fluid mechanics. For example, particles accelerated beyond the speed of light in a refractive medium (where the speed of light is less than that in a vacuum, such as water) create visible shock effects, a phenomenon known as Cherenkov radiation.
Phenomena types
Below are a number of examples of shock waves, broadly grouped with similar shock phenomena:
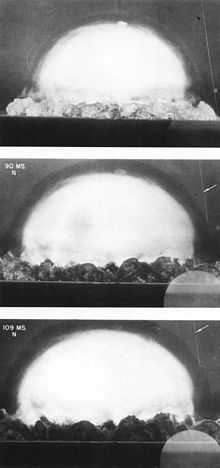
Moving shock
- Usually consists of a shockwave propagating into a stationary medium
- In this case, the gas ahead of the shock is stationary (in the laboratory frame) and the gas behind the shock can be supersonic in the laboratory frame. The shock propagates with a wavefront which is normal (at right angles) to the direction of flow. The speed of the shock is a function of the original pressure ratio between the two bodies of gas.
- Moving shocks are usually generated by the interaction of two bodies of gas at different pressure, with a shock wave propagating into the lower pressure gas and an expansion wave propagating into the higher pressure gas.
- Examples: Balloon bursting, Shock tube, shock wave from explosion.
Detonation wave
- A detonation wave is essentially a shock supported by a trailing exothermic reaction. It involves a wave travelling through a highly combustible or chemically unstable medium, such as an oxygen-methane mixture or a high explosive. The chemical reaction of the medium occurs following the shock wave, and the chemical energy of the reaction drives the wave forward.
- A detonation wave follows slightly different rules from an ordinary shock since it is driven by the chemical reaction occurring behind the shock wavefront. In the simplest theory for detonations, an unsupported, self-propagating detonation wave proceeds at the Chapman-Jouguet flow velocity. A detonation will also cause a shock of type 1, above to propagate into the surrounding air due to the overpressure induced by the explosion.
- When a shockwave is created by high explosives such as TNT (which has a detonation velocity of 6,900 m/s), it will always travel at high, supersonic velocity from its point of origin.


Bow shock (detached shock)
- These shocks are curved and form a small distance in front of the body. Directly in front of the body, they stand at 90 degrees to the oncoming flow and then curve around the body. Detached shocks allow the same type of analytic calculations as for the attached shock, for the flow near the shock. They are a topic of continuing interest, because the rules governing the shock's distance ahead of the blunt body are complicated and are a function of the body's shape. Additionally, the shock standoff distance varies drastically with the temperature for a non-ideal gas, causing large differences in the heat transfer to the thermal protection system of the vehicle. See the extended discussion on this topic at Atmospheric reentry. These follow the "strong-shock" solutions of the analytic equations, meaning that for some oblique shocks very close to the deflection angle limit, the downstream Mach number is subsonic. See also bow shock or oblique shock
- Such a shock occurs when the maximum deflection angle is exceeded. A detached shock is commonly seen on blunt bodies, but may also be seen on sharp bodies at low Mach numbers.
- Examples: Space return vehicles (Apollo, Space shuttle), bullets, the boundary (Bow shock) of a magnetosphere. The name "bow shock" comes from the example of a bow wave, the detached shock formed at the bow (front) of a ship or boat moving through water, whose slow surface wave speed is easily exceeded (see ocean surface wave).
Attached shock
- These shocks appear as attached to the tip of sharp bodies moving at supersonic speeds.
- Examples: Supersonic wedges and cones with small apex angles.
- The attached shock wave is a classic structure in aerodynamics because, for a perfect gas and inviscid flow field, an analytic solution is available, such that the pressure ratio, temperature ratio, angle of the wedge and the downstream Mach number can all be calculated knowing the upstream Mach number and the shock angle. Smaller shock angles are associated with higher upstream Mach numbers, and the special case where the shock wave is at 90° to the oncoming flow (Normal shock), is associated with a Mach number of one. These follow the "weak-shock" solutions of the analytic equations.
In rapid granular flows
Shock waves can also occur in rapid flows of dense granular materials down inclined channels or slopes. Strong shocks in rapid dense granular flows can be studied theoretically and analyzed to compare with experimental data. Consider a configuration in which the rapidly moving material down the chute impinges on an obstruction wall erected perpendicular at the end of a long and steep channel. Impact leads to a sudden change in the flow regime from a fast moving supercritical thin layer to a stagnant thick heap. This flow configuration is particularly interesting because it is analogous to some hydraulic and aerodynamic situations associated with flow regime changes from supercritical to subcritical flows.
In astrophysics
Astrophysical environments feature many different types of shock waves. Some common examples are supernovae shock waves or blast waves travelling through the interstellar medium, the bow shock caused by the Earth's magnetic field colliding with the solar wind and shock waves caused by galaxies colliding with each other. Another interesting type of shock in astrophysics is the quasi-steady reverse shock or termination shock that terminates the ultra relativistic wind from young pulsars.
Meteor entering events

The Tunguska event and the 2013 Russian meteor event are the best documented evidence of the shock wave produced by a massive meteoroid.
When the 2013 meteor entered into the Earth’s atmosphere with an energy release equivalent to 100 or more kilotons of TNT, dozens of times more powerful than the atomic bomb dropped on Hiroshima, the meteor's shock wave produced damages as in a supersonic jet's flyby (directly underneath the meteor's path) and as a detonation wave, with the circular shock wave centred at the meteor explosion, causing multiple instances of broken glass in the city of Chelyabinsk and neighbouring areas (pictured).
Technological applications
In the examples below, the shock wave is controlled, produced by (ex. airfoil) or in the interior of a technological device, like a turbine.
Recompression shock
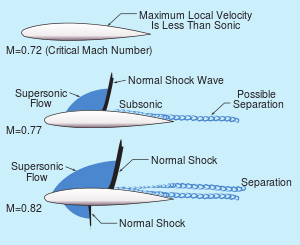
- These shocks appear when the flow over a transonic body is decelerated to subsonic speeds.
- Examples: Transonic wings, turbines
- Where the flow over the suction side of a transonic wing is accelerated to a supersonic speed, the resulting re-compression can be by either Prandtl-Meyer compression or by the formation of a normal shock. This shock is of particular interest to makers of transonic devices because it can cause separation of the boundary layer at the point where it touches the transonic profile. This can then lead to full separation and stall on the profile, higher drag, or shock-buffet, a condition where the separation and the shock interact in a resonance condition, causing resonating loads on the underlying structure.
Pipe flow
- This shock appears when supersonic flow in a pipe is decelerated.
- Examples:
- In this case the gas ahead of the shock is supersonic (in the laboratory frame), and the gas behind the shock system is either supersonic (oblique shocks) or subsonic (a normal shock) (Although for some oblique shocks very close to the deflection angle limit, the downstream Mach number is subsonic.) The shock is the result of the deceleration of the gas by a converging duct, or by the growth of the boundary layer on the wall of a parallel duct.
Combustion engines
The wave disk engine (also named "Radial Internal Combustion Wave Rotor") is a kind of pistonless rotary engine that utilizes shock waves to transfer energy between a high-energy fluid to a low-energy fluid, thereby increasing both temperature and pressure of the low-energy fluid.
Shock capturing and detection
Advanced techniques are needed to capture shock waves and to detect shock waves in both numerical computations and experimental observations.[4]
Computational fluid dynamics is commonly used to obtain the flow field with shock waves. Though shock waves are sharp discontinuities, in numerical solutions of fluid flow with discontinuities (shock wave, contact discontinuity or slip line), the shock wave can be smoothed out by low-order numerical method (due to numerical dissipation) or there are spurious oscillations near shock surface by high-order numerical method (due to Gibbs phenomena).
There exist some other discontinuities in fluid flow than the shock wave. The slip surface (3D) or slip line (2D) is a plane across which the tangent velocity is discontinuous, while pressure and normal velocity are continuous. Across the contact discontinuity, the pressure and velocity are continuous and the density is discontinuous. A strong expansion wave or shear layer may also contain high gradient regions which appear to be a discontinuity. Some common features of these flow structures and shock waves and the insufficient aspects of numerical and experimental tools lead to two important problems in practices: (1) some shock waves can not be detected or their positions are wrong detected, (2) some flow structures which are not shock waves are wrongly detected to be shock waves.
In fact, correct capturing and detection of shock waves are important since shock waves have the following influences: (1) causing loss of total pressure, which may be a concern related to scramjet engine performance, (2)providing lift for wave-rider configuration, as the oblique shock wave at lower surface of the vehicle can produce high pressure to generate lift, (3)leading to wave drag of high-speed vehicle which is harmful to vehicle performance, (4)inducing severe pressure load and heat flux, e.g. the Type IV shock–shock interference could yield a 17 times heating increase at vehicle surface, (5)interacting with other structures, such as boundary layers, to produce new flow structures such as flow separation, transition, etc.
See also
- Atmospheric focusing
- Atmospheric reentry
- Čerenkov radiation
- Explosion
- Hydraulic jump
- Joule–Thomson effect[5]
- Kerner’s breakdown minimization principle
- Mach wave
- Magnetopause
- Moreton wave
- Normal shock tables
- Oblique shock
- Prandtl–Meyer expansion fan
- Shocks and Discontinuities (MHD)
- Shock (mechanics)
- Sonic boom
- Three-phase traffic theory
- Traffic congestion: Reconstruction with Kerner's three-phase theory
- Supercritical airfoil
- Undercompressive shock wave
- Unstart
- Shock diamond
References
- ↑ Anderson, John D. Jr. (January 2001) [1984], Fundamentals of Aerodynamics (3rd ed.), McGraw-Hill Science/Engineering/Math, ISBN 0-07-237335-0
- ↑ [Introduction To Fluid Mechanics Fourth Edition, Robert W. Fox, Alan T. McDonald ISBN 0-471-54852-9]
- ↑ Settles, Gary S. (2006), High-speed Imaging of Shock Wave, Explosions and Gunshots 94 (1), American Scientist, pp. 22–31
- ↑ Wu ZN,Xu YZ,etc (2013), Review of shock wave detection method in CFD post-processing 26 (3), Chinese Journal of Aeronautics, pp. 501–513
- ↑ Hoover, Wm G., Carol G. Hoover, and Karl P. Travis. "Shock-Wave Compression and Joule-Thomson Expansion." Physical review letters 112.14 (2014): 144504.
External links
| Wikimedia Commons has media related to Shock waves. |
- NASA Glenn Research Center information on:
- Selkirk college: Aviation intranet: High speed (supersonic) flight
- Fundamentals of compressible flow, 2007
- KB Commercial finite-element educational software to simulate shocks and detonations.
Further reading
- Krehl, Peter O. K. (2011), "Shock wave physics and detonation physics — a stimulus for the emergence of numerous new branches in science and engineering", European Physical Journal H 36: 85, Bibcode:2011EPJH...36...85K, doi:10.1140/epjh/e2011-10037-x.