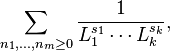Shintani zeta function
For the Shintani zeta function of a vector space, see Prehomogeneous vector space.
In mathematics, a Shintani zeta function or Shintani L-function is a generalization of the Riemann zeta function. They were first studied by Takuro Shintani (1976). They include Hurwitz zeta functions, Barnes zeta functions, and Witten zeta functions as special cases.
Definition
The Shintani zeta function of (s1, ..., sk) is given by
where each Lj is an inhomogeneous linear function of (n1, ... ,nm). The special case when k = 1 is the Barnes zeta function.
References
- Hida, Haruzo (1993), Elementary theory of L-functions and Eisenstein series, London Mathematical Society Student Texts 26, Cambridge University Press, ISBN 978-0-521-43411-9, MR 1216135, Zbl 0942.11024
- Shintani, Takuro (1976), "On evaluation of zeta functions of totally real algebraic number fields at non-positive integers", Journal of the Faculty of Science. University of Tokyo. Section IA. Mathematics 23 (2): 393–417, ISSN 0040-8980, MR 0427231, Zbl 0349.12007