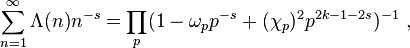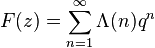Shimura correspondence
In number theory, the Shimura correspondence is a correspondence between modular forms F of half integral weight k+1/2, and modular forms f of even weight 2k, discovered by Goro Shimura (1973). It has the property that the eigenvalue of a Hecke operator Tn2 on F is equal to the eigenvalue of Tn on f.
Let  be a holomorphic cusp form with weight
be a holomorphic cusp form with weight 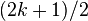 and character
and character 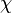 . For any prime number p, let
. For any prime number p, let
where 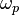 's are the eigenvalues of the Hecke operators
's are the eigenvalues of the Hecke operators 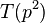 determined by p.
determined by p.
Using the functional equation of L-function, Shimura showed that
is a holomorphic modular function with weight 2k and character 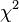 .
.
References
- Bump, D. (2001), "Shimura correspondence", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Shimura, Goro (1973), "On modular forms of half integral weight", Annals of Mathematics. Second Series 97: 440–481, ISSN 0003-486X, JSTOR 1970831, MR 0332663