Shilov boundary
In functional analysis, a branch of mathematics, the Shilov boundary is the smallest closed subset of the structure space of a commutative Banach algebra where an analog of the maximum modulus principle holds. It is named after its discoverer, Georgii Evgen'evich Shilov.
Precise definition and existence
Let 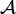 be a commutative Banach algebra and let
be a commutative Banach algebra and let 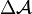 be its structure space equipped with the relative weak*-topology of the dual
be its structure space equipped with the relative weak*-topology of the dual 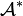 . A closed (in this topology) subset
. A closed (in this topology) subset 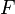 of
of 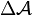 is called a boundary of
is called a boundary of 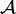 if
if 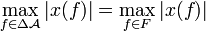 for all
for all 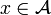 .
The set
.
The set 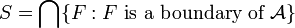 is called the Shilov boundary. It has been proved by Shilov[1] that
is called the Shilov boundary. It has been proved by Shilov[1] that  is a boundary of
is a boundary of 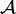 .
.
Thus one may also say that Shilov boundary is the unique set 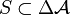 which satisfies
which satisfies
 is a boundary of
is a boundary of 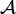 , and
, and- whenever
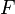 is a boundary of
is a boundary of 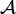 , then
, then 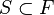 .
.
Examples
- Let
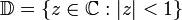 be the open unit disc in the complex plane and let
be the open unit disc in the complex plane and let
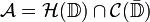 be the disc algebra, i.e. the functions holomorphic in
be the disc algebra, i.e. the functions holomorphic in 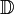 and continuous in the closure of
and continuous in the closure of 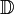 with supremum norm and usual algebraic operations. Then
with supremum norm and usual algebraic operations. Then 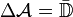 and
and 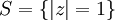 .
.
References
- Hazewinkel, Michiel, ed. (2001), "Bergman-Shilov boundary", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Notes
- ↑ Theorem 4.15.4 in Einar Hille, Ralph S. Phillips: Functional analysis and semigroups. -- AMS, Providence 1957.
See also
- James boundary