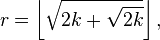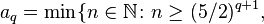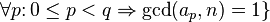Shellsort
 Shellsort with gaps 23, 10, 4, 1 in action. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst case performance | O(n2) |
| Best case performance | O(n log2 n) |
| Average case performance | depends on gap sequence |
| Worst case space complexity | О(n) total, O(1) auxiliary |
Shellsort, also known as Shell sort or Shell's method, is an in-place comparison sort. It can be seen as either a generalization of sorting by exchange (bubble sort) or sorting by insertion (insertion sort).[1] The method starts by sorting pairs of elements far apart from each other, then progressively reducing the gap between elements to be compared. Starting with far apart elements can move some out-of-place elements into position faster than a simple nearest neighbor exchange. Donald Shell published the first version of this sort in 1959.[2][3] The running time of Shellsort is heavily dependent on the gap sequence it uses. For many practical variants, determining their time complexity remains an open problem.
Description
Shellsort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every hth element gives a sorted list. Such a list is said to be h-sorted. Equivalently, it can be thought of as h interleaved lists, each individually sorted.[4] Beginning with large values of h, this rearrangement allows elements to move long distances in the original list, reducing large amounts of disorder quickly, and leaving less work for smaller h-sort steps to do.[5] If the file is then k-sorted for some smaller integer k, then the file remains h-sorted. Following this idea for a decreasing sequence of h values ending in 1 is guaranteed to leave a sorted list in the end.[4]
An example run of Shellsort with gaps 5, 3 and 1 is shown below.

The first pass, 5-sorting, performs insertion sort on separate subarrays (a1, a6, a11), (a2, a7, a12), (a3, a8), (a4, a9), (a5, a10). For instance, it changes the subarray (a1, a6, a11) from (62, 17, 25) to (17, 25, 62). The next pass, 3-sorting, performs insertion sort on the subarrays (a1, a4, a7, a10), (a2, a5, a8, a11), (a3, a6, a9, a12). The last pass, 1-sorting, is an ordinary insertion sort of the entire array (a1,..., a12).
As the example illustrates, the subarrays that Shellsort operates on are initially short; later they are longer but almost ordered. In both cases insertion sort works efficiently.
Shellsort is unstable: it may change the relative order of elements with equal values. It is an adaptive sorting algorithm in that it executes faster when the input is partially sorted.
Pseudocode
Using Marcin Ciura's gap sequence, with an inner insertion sort.
# Sort an array a[0...n-1].
gaps = [701, 301, 132, 57, 23, 10, 4, 1]
# Start with the largest gap and work down to a gap of 1
foreach (gap in gaps)
{
# Do a gapped insertion sort for this gap size.
# The first gap elements a[0..gap-1] are already in gapped order
# keep adding one more element until the entire array is gap sorted
for (i = gap; i < n; i += 1)
{
# add a[i] to the elements that have been gap sorted
# save a[i] in temp and make a hole at position i
temp = a[i]
# shift earlier gap-sorted elements up until the correct location for a[i] is found
for (j = i; j >= gap and a[j - gap] > temp; j -= gap)
{
a[j] = a[j - gap]
}
# put temp (the original a[i]) in its correct location
a[j] = temp
}
}
Gap sequences
The question of deciding which gap sequence to use is difficult. Every gap sequence that contains 1 yields a correct sort; however, the properties of thus obtained versions of Shellsort may be very different.
The table below compares most proposed gap sequences published so far. Some of them have decreasing elements that depend on the size of the sorted array (N). Others are increasing infinite sequences, whose elements less than N should be used in reverse order.
General term (k ≥ 1) Concrete gaps Worst-case
time complexityAuthor and year of publication 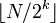
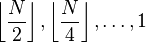
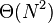 [when N=2p]
[when N=2p]Shell, 1959[2] 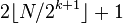
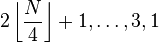
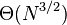
Frank & Lazarus, 1960[6] 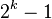
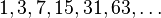
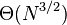
Hibbard, 1963[7] 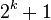 , prefixed with 1
, prefixed with 1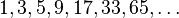
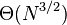
Papernov & Stasevich, 1965[8] successive numbers of the form 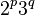
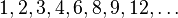
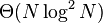
Pratt, 1971[9] 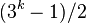 , not greater than
, not greater than 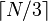
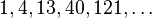
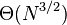
Pratt, 1971[9] 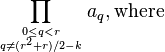
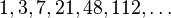
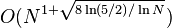
Incerpi & Sedgewick, 1985,[10] Knuth[1] 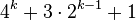 , prefixed with 1
, prefixed with 1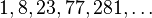
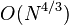
Sedgewick, 1986[4] 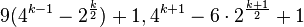
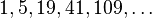
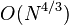
Sedgewick, 1986[4] 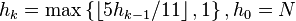
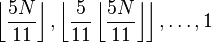
? Gonnet & Baeza-Yates, 1991[11] 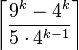
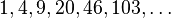
? Tokuda, 1992[12] unknown 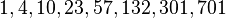
? Ciura, 2001[13]
When the binary representation of N contains many consecutive zeroes, Shellsort using Shell's original gap sequence makes Θ(N2) comparisons in the worst case. For instance, this case occurs for N equal to a power of two when elements greater and smaller than the median occupy odd and even positions respectively, since they are compared only in the last pass.
Although it has higher complexity than the O(NlogN) that is optimal for comparison sorts, Pratt's version lends itself to sorting networks and has the same asymptotic gate complexity as Batcher's bitonic sorter.
Gonnet and Baeza-Yates observed that Shellsort makes the fewest comparisons on average when the ratios of successive gaps are roughly equal to 2.2.[11] This is why their sequence with ratio 2.2 and Tokuda's sequence with ratio 2.25 prove efficient. However, it is not known why this is so. Sedgewick recommends to use gaps that have low greatest common divisors or are pairwise coprime.[14]
With respect to the average number of comparisons, the best known gap sequences are 1, 4, 10, 23, 57, 132, 301, 701 and similar, with gaps found experimentally. Optimal gaps beyond 701 remain unknown, but good results can be obtained by extending the above sequence according to the recursive formula 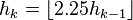 .
.
Tokuda's sequence, defined by the simple formula  , where
, where 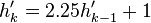 ,
, 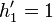 , can be recommended for practical applications.
, can be recommended for practical applications.
Computational complexity
The following property holds: after h2-sorting of any h1-sorted array, the array remains h1-sorted.[15] Every h1-sorted and h2-sorted array is also (a1h1+a2h2)-sorted, for any nonnegative integers a1 and a2. The worst-case complexity of Shellsort is therefore connected with the Frobenius problem: for given integers h1,..., hn with gcd = 1, the Frobenius number g(h1,..., hn) is the greatest integer that cannot be represented as a1h1+ ... +anhn with nonnegative integer a1,..., an. Using known formulae for Frobenius numbers, we can determine the worst-case complexity of Shellsort for several classes of gap sequences.[16] Proven results are shown in the above table.
With respect to the average number of operations, none of proven results concerns a practical gap sequence. For gaps that are powers of two, Espelid computed this average as 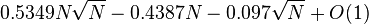 .[17] Knuth determined the average complexity of sorting an N-element array with two gaps (h, 1) to be
.[17] Knuth determined the average complexity of sorting an N-element array with two gaps (h, 1) to be 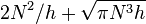 .[1] It follows that a two-pass Shellsort with h = Θ(N1/3) makes on average O(N5/3) comparisons. Yao found the average complexity of a three-pass Shellsort.[18] His result was refined by Janson and Knuth:[19] the average number of comparisons made during a Shellsort with three gaps (ch, cg, 1), where h and g are coprime, is
.[1] It follows that a two-pass Shellsort with h = Θ(N1/3) makes on average O(N5/3) comparisons. Yao found the average complexity of a three-pass Shellsort.[18] His result was refined by Janson and Knuth:[19] the average number of comparisons made during a Shellsort with three gaps (ch, cg, 1), where h and g are coprime, is 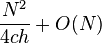 in the first pass,
in the first pass, 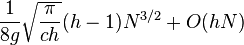 in the second pass and
in the second pass and 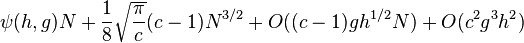 in the third pass. ψ(h, g) in the last formula is a complicated function asymptotically equal to
in the third pass. ψ(h, g) in the last formula is a complicated function asymptotically equal to 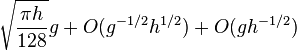 . In particular, when h = Θ(N7/15) and g = Θ(N1/5), the average time of sorting is O(N23/15).
. In particular, when h = Θ(N7/15) and g = Θ(N1/5), the average time of sorting is O(N23/15).
Based on experiments, it is conjectured that Shellsort with Hibbard's gap sequence runs in O(N5/4) average time,[1] and that Gonnet and Baeza-Yates's sequence requires on average 0.41NlnN(ln lnN+1/6) element moves.[11] Approximations of the average number of operations formerly put forward for other sequences fail when sorted arrays contain millions of elements.
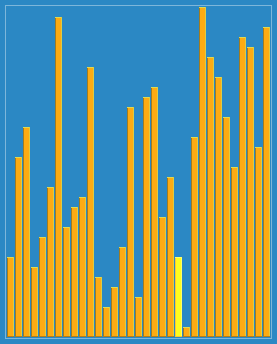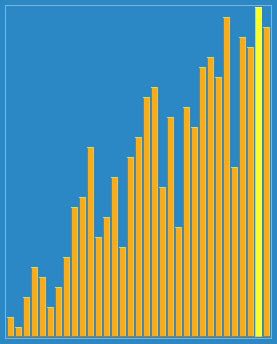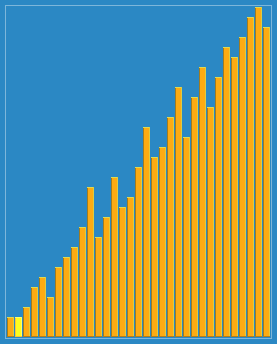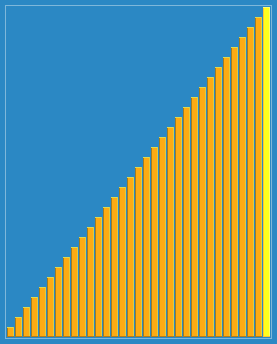
The graph below shows the average number of element comparisons in various variants of Shellsort, divided by the theoretical lower bound, i.e. log2N!, where the sequence 1, 4, 10, 23, 57, 132, 301, 701 has been extended according to the formula 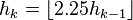 .
.
Applying the theory of Kolmogorov complexity, Jiang, Li, and Vitányi proved the following lower bounds for the order of the average number of operations in an m-pass Shellsort: Ω(mN1+1/m) when m≤log2N and Ω(mN) when m>log2N.[20] Therefore Shellsort has prospects of running in an average time that asymptotically grows like NlogN only when using gap sequences whose number of gaps grows in proportion to the logarithm of the array size. It is, however, unknown whether Shellsort can reach this asymptotic order of average-case complexity, which is optimal for comparison sorts.
The worst-case complexity of any version of Shellsort is of higher order: Plaxton, Poonen, and Suel showed that it grows at least as rapidly as Ω(N(logN/log logN)2).[21]
Applications
Shellsort is now rarely used in serious applications. It performs more operations and has higher cache miss ratio than quicksort. However, since it can be implemented using little code and does not use the call stack, some implementations of the qsort function in the C standard library targeted at embedded systems use it instead of quicksort. Shellsort is, for example, used in the uClibc library.[22] For similar reasons, an implementation of Shellsort is present in the Linux kernel.[23]
Shellsort can also serve as a sub-algorithm of introspective sort, to sort short subarrays and to prevent a pathological slowdown when the recursion depth exceeds a given limit. This principle is employed, for instance, in the bzip2 compressor.[24]
See also
References
- ↑ 1.0 1.1 1.2 1.3 Knuth, Donald E. (1997). "Shell's method". The Art of Computer Programming. Volume 3: Sorting and Searching (2nd ed.). Reading, Massachusetts: Addison-Wesley. pp. 83–95. ISBN 0-201-89685-0.
- ↑ 2.0 2.1 Shell, D. L. (1959). "A High-Speed Sorting Procedure" (PDF). Communications of the ACM 2 (7): 30–32. doi:10.1145/368370.368387.
- ↑ Some older textbooks and references call this the "Shell-Metzner" sort after Marlene Metzner Norton, but according to Metzner, "I had nothing to do with the sort, and my name should never have been attached to it." See "Shell sort". National Institute of Standards and Technology. Retrieved 2007-07-17.
- ↑ 4.0 4.1 4.2 4.3 Sedgewick, Robert (1998). Algorithms in C 1 (3rd ed.). Addison-Wesley. pp. 273–281. ISBN 0-201-31452-5.
- ↑ Kernighan, Brian W.; Ritchie, Dennis M. (1996). The C Programming Language (2nd ed.). Prentice Hall. p. 62. ISBN 7-302-02412-X.
- ↑ Frank, R. M.; Lazarus, R. B. (1960). "A High-Speed Sorting Procedure". Communications of the ACM 3 (1): 20–22. doi:10.1145/366947.366957.
- ↑ Hibbard, Thomas N. (1963). "An Empirical Study of Minimal Storage Sorting". Communications of the ACM 6 (5): 206–213. doi:10.1145/366552.366557.
- ↑ Papernov, A. A.; Stasevich, G. V. (1965). "A Method of Information Sorting in Computer Memories" (PDF). Problems of Information Transmission 1 (3): 63–75.
- ↑ 9.0 9.1 Pratt, Vaughan Ronald (1979). Shellsort and Sorting Networks (Outstanding Dissertations in the Computer Sciences). Garland. ISBN 0-8240-4406-1.
- ↑ Incerpi, Janet; Sedgewick, Robert (1985). "Improved Upper Bounds on Shellsort". Journal of Computer and System Sciences 31 (2): 210–224. doi:10.1016/0022-0000(85)90042-x.
- ↑ 11.0 11.1 11.2 Gonnet, Gaston H.; Baeza-Yates, Ricardo (1991). "Shellsort". Handbook of Algorithms and Data Structures: In Pascal and C (2nd ed.). Reading, Massachusetts: Addison-Wesley. pp. 161–163. ISBN 0-201-41607-7.
- ↑ Tokuda, Naoyuki (1992). "An Improved Shellsort". In van Leeuven, Jan. Proceedings of the IFIP 12th World Computer Congress on Algorithms, Software, Architecture. Amsterdam: North-Holland Publishing Co. pp. 449–457. ISBN 0-444-89747-X.
- ↑ Ciura, Marcin (2001). "Best Increments for the Average Case of Shellsort". In Freiwalds, Rusins. Proceedings of the 13th International Symposium on Fundamentals of Computation Theory (PDF). London: Springer-Verlag. pp. 106–117. ISBN 3-540-42487-3.
- ↑ Sedgewick, Robert (1998). "Shellsort". Algorithms in C++, Parts 1-4: Fundamentals, Data Structure, Sorting, Searching. Reading, Massachusetts: Addison-Wesley. pp. 285–292. ISBN 0-201-35088-2.
- ↑ Gale, David; Karp, Richard M. (1972). "A Phenomenon in the Theory of Sorting". Journal of Computer and System Sciences 6 (2): 103–115. doi:10.1016/S0022-0000(72)80016-3.
- ↑ Selmer, Ernst S. (1989). "On Shellsort and the Frobenius Problem". BIT Numerical Mathematics 29 (1): 37–40. doi:10.1007/BF01932703.
- ↑ Espelid, Terje O. (1973). "Analysis of a Shellsort Algorithm". BIT Numerical Mathematics 13 (4): 394–400. doi:10.1007/BF01933401.
- ↑ Yao, Andrew Chi-Chih (1980). "An Analysis of (h, k, 1)-Shellsort". Journal of Algorithms 1 (1): 14–50. doi:10.1016/0196-6774(80)90003-6.
- ↑ Janson, Svante; Knuth, Donald E. (1997). "Shellsort with Three Increments". Random Structures and Algorithms 10 (1-2): 125–142. arXiv:cs/9608105. doi:10.1002/(SICI)1098-2418(199701/03)10:1/2<125::AID-RSA6>3.0.CO;2-X. CiteSeerX: 10
.1 ..1 .54 .9911 - ↑ Jiang, Tao; Li, Ming; Vitányi, Paul (2000). "A Lower Bound on the Average-Case Complexity of Shellsort". Journal of the ACM 47 (5): 905–911. doi:10.1145/355483.355488. CiteSeerX: 10
.1 ..1 .6 .6508 - ↑ Plaxton, C. Greg; Poonen, Bjarne; Suel, Torsten (1992). "Improved Lower Bounds for Shellsort". Annual Symposium on Foundations of Computer Science 33: 226–235. doi:10.1109/SFCS.1992.267769. CiteSeerX: 10
.1 ..1 .43 .1393 - ↑ Novoa, Manuel III. "libc/stdlib/stdlib.c". Retrieved 2014-10-29.
- ↑ "kernel/groups.c". Retrieved 2012-05-05.
- ↑ Julian Seward. "bzip2/blocksort.c". Retrieved 2011-03-30.
Bibliography
- Knuth, Donald E. (1997). "Shell's method". The Art of Computer Programming. Volume 3: Sorting and Searching (2nd ed.). Reading, Massachusetts: Addison-Wesley. pp. 83–95. ISBN 0-201-89685-0.
- Analysis of Shellsort and Related Algorithms, Robert Sedgewick, Fourth European Symposium on Algorithms, Barcelona, September 1996.
External links
| The Wikibook Algorithm implementation has a page on the topic of: Shell sort |
| ||||||||||||||||||||||||||||||||||||||