Shelling (topology)

In mathematics, a shelling of a simplicial complex is a way of gluing it together from its maximal simplices (simplices that are not a face of another simplex) in a well-behaved way. A complex admitting a shelling is called shellable.

Definition

A d-dimensional simplicial complex is called pure if its maximal simplices all have dimension d. Let 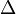$\Delta$ be a finite or countably infinite simplicial complex. An ordering 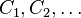$C_1,C_2,\ldots$ of the maximal simplices of 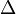$\Delta$ is a shelling if the complex 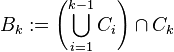$B_k:=\left(\bigcup_{i=1}^{k-1}C_i\right)\cap C_k$ is pure and 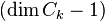$(\dim C_k-1)$ -dimensional for all 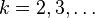$k=2,3,\ldots$ . That is, the "new" simplex 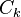$C_k$ meets the previous simplices along some union 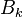$B_k$ of top-dimensional simplices of the boundary of 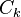$C_k$ . 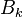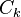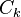If $B_k$ is the entire boundary of $C_k$ then $C_k$ is called spanning.

For 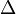$\Delta$ not necessarily countable, one can define a shelling as a well-ordering of the maximal simplices of 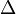$\Delta$ having analogous properties.

Properties

A shellable complex is homotopy equivalent to a wedge sum of spheres, one for each spanning simplex and of corresponding dimension.
A shellable complex may admit many different shellings, but the number of spanning simplices, and their dimensions, do not depend on the choice of shelling. This follows from the previous property.

Examples

Every Coxeter complex, and more generally every building, is shellable.^[1]

There is an unshellable triangulation of the tetrahedron.^[2]

References

Dmitry Kozlov (2008). Combinatorial Algebraic Topology. Berlin: Springer. ISBN 978-3-540-71961-8.

↑ Björner, Anders (June 1984). "Some combinatorial and algebraic properties of Coxeter complexes and Tits buildings". Advances in Mathematics 52 (3): 173–212. doi:10.1016/0001-8708(84)90021-5. ISSN 0001-8708.
↑ Rudin, M.E. (1958-02-14). "An unshellable triangulation of a tetrahedron". Bull. Am. Math. Soc. 64 (3): 90–91. doi:10.1090/s0002-9904-1958-10168-8. ISSN 1088-9485.