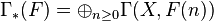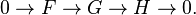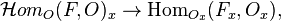Sheaf of modules
In mathematics, a sheaf of O-modules or simply an O-module over a ringed space (X, O) is a sheaf F such that, for any open subset U of X, F(U) is an O(U)-module and the restriction maps F(U) →F(V) are compatible with the restriction maps O(U) →O(V): the restriction of fs is the restriction of f times that of s for any f in O(U) and s in F(U).
The standard case is when X is a scheme and O its structure sheaf. If O is the constant sheaf 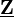 , then a sheaf of O-modules are the same as a sheaf of abelian groups (i.e., abelian sheaf).
, then a sheaf of O-modules are the same as a sheaf of abelian groups (i.e., abelian sheaf).
If X is the prime spectrum of a ring R, then any R-module defines an OX-module (called an associated sheaf) in a natural way. Similarly, if R is a graded ring and X is the Proj of R, then any graded module defines an OX-module in a natural way. O-modules arising in such a fashion are examples of quasi-coherent sheaves, and in fact, on affine or projective schemes, all quasi-coherent sheaves are obtained this way.
Sheaves of modules over a ringed space form an abelian category.[1] Moreover, this category has enough injectives,[2] and consequently one can and does define the sheaf cohomology 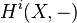 as the i-th right derived functor of the global section functor
as the i-th right derived functor of the global section functor 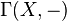 .
.
Operations
Let (X, O) be a ringed space. If F and G are O-modules, then their tensor product, denoted by
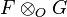 or
or 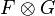 ,
,
is the O-module that is the sheaf associated to the presheaf 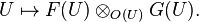 (To see that sheafification cannot be avoided, compute the global sections of
(To see that sheafification cannot be avoided, compute the global sections of 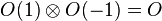 where O(1) is Serre's twisting sheaf on a projective space.)
where O(1) is Serre's twisting sheaf on a projective space.)
Similarly, if F and G are O-modules, then
denotes the O-module that is the sheaf 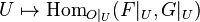 .[3] In particular, the O-module
.[3] In particular, the O-module
is called the dual module of F and is denoted by 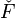 . Note: for any O-modules E, F, there is a canonical homomorphism
. Note: for any O-modules E, F, there is a canonical homomorphism
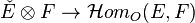 ,
,
which is an isomorphism if E is a locally free sheaf of finite rank. In particular, if L is locally free of rank one (such L is called an invertible sheaf or a line bundle),[4] then this reads:
implying the isomorphism classes of invertible sheaves form a group. This group is called the Picard group of X and is canonically identified with the first cohomology group 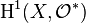 (by the standard argument with Čech cohomology).
(by the standard argument with Čech cohomology).
If E is a locally free sheaf of finite rank, then there is an O-linear map 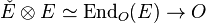 given by the pairing; it is called the trace map of E.
given by the pairing; it is called the trace map of E.
For any O-module F, the tensor algebra, exterior algebra and symmetric algebra of F are defined in the same way. For example, the k-th exterior power
is the sheaf associated to the presheaf 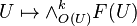 . If F is locally free of rank n, then
. If F is locally free of rank n, then 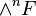 is called the determinant line bundle (though technically invertible sheaf) of F, denoted by det(F). There is a natural perfect paring:
is called the determinant line bundle (though technically invertible sheaf) of F, denoted by det(F). There is a natural perfect paring:
Let f: (X, O) →(X ', O ') be a morphism of ringed spaces. If F is an O-module, then the direct image sheaf 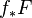 is an O '-module through the natural map O ' →f*O (such a natural map is part of the data of a morphism of ringed spaces.)
is an O '-module through the natural map O ' →f*O (such a natural map is part of the data of a morphism of ringed spaces.)
If G is an O '-module, then the module inverse image 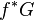 of G is the O-module given as the tensor product of modules:
of G is the O-module given as the tensor product of modules:
where 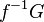 is the inverse image sheaf of G and
is the inverse image sheaf of G and 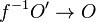 is obtained from
is obtained from 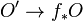 by adjuction.
by adjuction.
There is an adjoint relation between 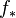 and
and 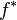 : for any O-module F and O'-module G,
: for any O-module F and O'-module G,
as abelian group. There is also the projection formula: for an O-module F and a locally free O'-module E of finite rank,
Properties
Let (X, O) be a ringed space. An O-module F is said to be generated by global sections if there is a surjection of O-modules:
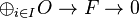 .
.
Explicitly, this means that there are global sections si of F such that the images of si in each stalk Fx generates Fx as Ox-module.
An example of such a sheaf is that associated in algebraic geometry to an R-module M, R being any commutative ring, on the spectrum of a ring Spec(R). Another example: according to Cartan's theorem A, any coherent sheaf on a Stein manifold is spanned by global sections. (cf. Serre's theorem A below.) In the theory of schemes, a related notion is ample line bundle. (For example, if L is an ample line bundle, some power of it is generated by global sections.)
An injective O-module is flasque (i.e., all restrictions maps F(U) → F(V) are surjective.)[5] Since a flasque sheaf is acyclic, this implies that the i-th right derived functor of the global section functor 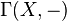 coincides with the usual i-th cohomology.[6]
coincides with the usual i-th cohomology.[6]
Sheaf associated to a module
Let R be a ring and M an R-module. Let also 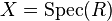 . Then there is an
. Then there is an 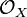 -module
-module 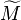 whose stalk
whose stalk 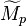 at a prime ideal p is isomorphic to the localization Mp of M at p as Op = Rp-module. Also,
at a prime ideal p is isomorphic to the localization Mp of M at p as Op = Rp-module. Also, 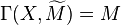 .
.
The functor 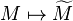 is an equivalence from the category of R-modules to the category of quasi-coherent
is an equivalence from the category of R-modules to the category of quasi-coherent 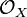 -modules with
-modules with 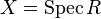 ; the inverse is the global section functor
; the inverse is the global section functor 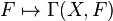 .[7] Suppose X is a Noetherian scheme or equivalently R is a Noetherian ring. Then the functor
.[7] Suppose X is a Noetherian scheme or equivalently R is a Noetherian ring. Then the functor 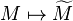 is an equivalence from the category of finitely generated R-modules to the category of coherent
is an equivalence from the category of finitely generated R-modules to the category of coherent 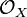 -modules.
-modules.
There is a graded analog of the above construction and equivalence. Let R be a graded ring generated by degree-one elements as R0-algebra (R0 means the degree-zero piece) and M a graded R-module. Let X be the Proj of R (so X is a projective scheme). Then there is an O-module 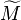 such that for any homogeneous element f of positive degree of R, there is a natural isomorphism
such that for any homogeneous element f of positive degree of R, there is a natural isomorphism
as sheaves of modules on the affine scheme ![\{f \ne 0\} = \operatorname{Spec}(R[f^{-1}]_0)](../I/m/799d29e32fa4823f2dab617033c790b7.png) ;[8] in fact, this defines
;[8] in fact, this defines 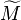 by gluing.
by gluing.
Example: Let R(1) be the graded R-module given by R(1)n = Rn+1. Then 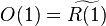 is called Serre's twisting sheaf (the dual of the tautological line bundle.)
is called Serre's twisting sheaf (the dual of the tautological line bundle.)
If F is an O-module on X, then, writing 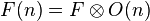 , the direct sum
, the direct sum
is a graded R-module. Then there is a canonical homomorphism:
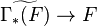 ,
,
which is an isomorphism if and only if F is quasi-coherent.
Serre's theorem A states that if R is a Noetherian ring and F is coherent, then for sufficiently large n, F(n) is generated by finitely many global sections. Moreover,
- (a) For each i, Hi(X, F) is finitely generated over R0, and
- (b) (Serre's theorem B) There is an integer n0, depending on F, such that
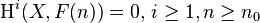 .
.
Sheaf extension
Let (X, O) be a ringed space, and let F, H be sheaves of O-modules on X. An extension of H by F is a short exact sequence of O-modules
As with group extensions, if we fix F and H, then all equivalence classes of extensions of H by F form an abelian group (cf. Baer sum), which is isomorphic to the Ext group 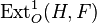 , where the identity element in
, where the identity element in 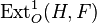 corresponds to the trivial extension.
corresponds to the trivial extension.
In the case where H is O, we have
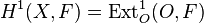 ,[9]
,[9]
so the group of extensions of 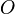 by F is also isomorphic to the first sheaf cohomology group with coefficients in F.
by F is also isomorphic to the first sheaf cohomology group with coefficients in F.
Note: Some authors, notably Hartshorne, drop the subscript O.
Examples
- If F is an O-module, then an O-submodule of F is called the ideal or ideal sheaf of O.
- Let X be a smooth variety of dimension n. Then the tangent sheaf of X is the dual of the cotangent sheaf
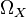 and the canonical sheaf
and the canonical sheaf 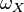 is the n-th exterior power (determinant) of
is the n-th exterior power (determinant) of 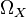 .
.
See also
- D-module (in place of O, one can also consider D, the sheaf of differential operators.)
- fractional ideal
- holomorphic vector bundle
Notes
- ↑ Vakil, Math 216: Foundations of algebraic geometry, 2.5.
- ↑ Hartshorne, Ch. III, Proposition 2.2.
- ↑ There is a canonical homomorphism:
- ↑ For coherent sheaves, having a tensor inverse is the same as being locally free of rank one; in fact, there is the following fact: if
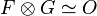 and if F is coherent, then F, G are locally free of rank one. (cf. EGA, Ch 0, 5.4.3.)
and if F is coherent, then F, G are locally free of rank one. (cf. EGA, Ch 0, 5.4.3.) - ↑ Hartshorne, Ch III, Lemma 2.4.
- ↑ see also: http://math.stackexchange.com/questions/447220/hartshornes-weird-definition-of-right-derived-functors-and-prop-iii-2-6/447234#447234
- ↑ Hartshorne, Ch II, Corollary 5.5.
- ↑ Hartshorne, Ch. II, Proposition 5.11.
- ↑ since both the sides are the right derived functors of the same functor
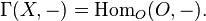
References
- Grothendieck, Alexandre; Dieudonné, Jean (1960). "Éléments de géométrie algébrique: I. Le langage des schémas". Publications Mathématiques de l'IHÉS 4. doi:10.1007/bf02684778. MR 0217083.
- Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
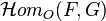
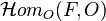
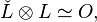
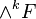
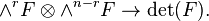
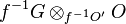
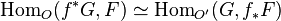
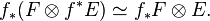
![\widetilde{M}|_{\{f \ne 0\}} \simeq (M[f^{-1}]_0)^{\sim}](../I/m/dd8f1381b5ba4b25b685448d6343590e.png)