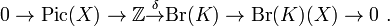Severi–Brauer variety
In mathematics, a Severi–Brauer variety over a field K is an algebraic variety V which becomes isomorphic to a projective space over an algebraic closure of K. The varieties are associated to central simple algebras in such a way that the algebra splits over K if and only if the variety has a point rational over K.[1] Francesco Severi (1932) studied these varieties, and they are also named after Richard Brauer because of their close relation to the Brauer group.
In dimension one, the Severi–Brauer varieties are conics. The corresponding central simple algebras are the quaternion algebras. The algebra (a,b)K corresponds to the conic C(a,b) with equation
and the algebra (a,b)K splits, that is, (a,b)K is isomorphic to a matrix algebra over K, if and only if C(a,b) has a point defined over K: this is in turn equivalent to C(a,b) being isomorphic to the projective line over K.[1][2]
Such varieties are of interest not only in diophantine geometry, but also in Galois cohomology. They represent (at least if K is a perfect field) Galois cohomology classes in
- H1(PGLn)
in the projective linear group, where n is the dimension of V. There is a short exact sequence
- 1 → GL1 → GLn → PGLn → 1
of algebraic groups. This implies a connecting homomorphism
- H1(PGLn) → H2(GL1)
at the level of cohomology. Here H2(GL1) is identified with the Brauer group of K, while the kernel is trivial because
- H1(GLn) = {1}
by an extension of Hilbert's Theorem 90.[3][4] Therefore the Severi–Brauer varieties can be faithfully represented by Brauer group elements, i.e. classes of central simple algebras.
Lichtenbaum showed that if X is a Severi–Brauer variety over K then there is an exact sequence
Here the map δ sends 1 to the Brauer class corresponding to X.[2]
As a consequence, we see that if the class of X has order d in the Brauer group then there is a divisor class of degree d on X. The associated linear system defines the d-dimensional embedding of X over a splitting field L.[5]
References
- ↑ 1.0 1.1 Jacobson (1996) p.113
- ↑ 2.0 2.1 Gille & Szamuely (2006) p.129
- ↑ Gille & Szamuely (2006) p.26
- ↑ Berhuy, Grégory (2010), An Introduction to Galois Cohomology and its Applications, London Mathematical Society Lecture Note Series 377, Cambridge University Press, p. 113, ISBN 0-521-73866-0, Zbl 1207.12003
- ↑ Gille & Szamuely (2006) p.131
- Artin, Michael (1982), "Brauer-Severi varieties", Brauer groups in ring theory and algebraic geometry (Wilrijk, 1981), Lecture Notes in Math. 917, Notes by A. Verschoren, Berlin, New York: Springer-Verlag, pp. 194–210, doi:10.1007/BFb0092235, ISBN 978-3-540-11216-7, MR 657430, Zbl 0536.14006
- Hazewinkel, Michiel, ed. (2001), "Brauer–Severi variety", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Gille, Philippe; Szamuely, Tamás (2006), "Severi–Brauer varieties", Central Simple Algebras and Galois Cohomology, Cambridge Studies in Advanced Mathematics 101, Cambridge University Press, pp. 114–134, ISBN 0-521-86103-9, MR 2266528, Zbl 1137.12001
- Jacobson, Nathan (1996), Finite-dimensional division algebras over fields, Berlin: Springer-Verlag, ISBN 3-540-57029-2, Zbl 0874.16002
- Saltman, David J. (1999), Lectures on division algebras, Regional Conference Series in Mathematics 94, Providence, RI: American Mathematical Society, ISBN 0-8218-0979-2, Zbl 0934.16013
- Severi, Francesco (1932), "Un nuovo campo di ricerche nella geometria sopra una superficie e sopra una varietà algebrica", Memorie della Reale Accademia d'Italia (in Italian) 3 (5), Reprinted in volume 3 of his collected works
Further reading
- Knus, Max-Albert; Merkurjev, Alexander; Rost, Markus; Tignol, Jean-Pierre (1998), The book of involutions, Colloquium Publications 44, With a preface by J. Tits, Providence, RI: American Mathematical Society, ISBN 0-8218-0904-0, MR MR1632779, Zbl 0955.16001