Serre's criterion on normality

In algebra, Serre's criterion on normality, introduced by Jean-Pierre Serre, gives necessary and sufficient conditions for a commutative Noetherian ring A to be a normal ring. The criterion involves the following two conditions for A:

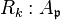$R_k: A_{\mathfrak{p}}$ is a regular local ring for any prime ideal 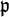$\mathfrak{p}$ of height ≤ k.
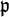$S_k: \operatorname{depth} A_{\mathfrak{p}} \ge \inf \{k, \operatorname{ht}(\mathfrak{p}) \}$ for any prime ideal $\mathfrak{p}$ .^[1]

The statement is:

A is a reduced ring $\Leftrightarrow R_0, S_1$ hold.
A is a normal ring 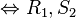$\Leftrightarrow R_1, S_2$ hold.
A is a Cohen–Macaulay ring $\Leftrightarrow S_k$ hold for all k.

Items 1, 3 trivially follow from the definitions. Item 2 is much deeper.

For an integral domain, the criterion is due to Krull. The general case is due to Serre.

Proof

Sufficiency

(After EGA IV. Theorem 5.8.6.)

Suppose A satisfies S₂ and R₁. Then A in particular satisfies S₁ and R₀; hence, it is reduced. If $\mathfrak{p}_i, \, 1 \le i \le r$ are the minimal prime ideals of A, then the total ring of fractions K of A is the direct product of the residue fields $\kappa(\mathfrak{p}_i) = Q(A/\mathfrak{p}_i)$ : see total ring of fractions of a reduced ring. 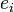That means we can write $1 = e_1 + \dots + e_r$ where $e_i$ are idempotents in $\kappa(\mathfrak{p}_i)$ and such that $e_i e_j = 0, \, i \ne j$ . 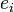Now, if A is integrally closed in K, then each $e_i$ is integral over A and so is in A; consequently, A is a direct product of integrally closed domains Ae_i's and we are done. Thus, it is enough to show that A is integrally closed in K.

For this end, suppose

(f/g)^n + a_1 (f/g)^{n-1} + \dots + a_n = 0

where all f, g, a_i's are in A and g is moreover a non-zerodivisor. We want to show:

f \in gA

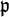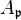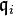Now, the condition S₂ says that $gA$ is unmixed of height one; i.e., each associated primes $\mathfrak{p}$ of $A/gA$ has height one. By the condition R₁, the localization $A_{\mathfrak{p}}$ is integrally closed and so $\phi(f) \in \phi(g)A_{\mathfrak{p}}$ , where $\phi: A \to A_{\mathfrak{p}}$ is the localization map, since the integral equation persists after localization. 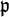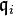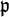If $gA = \cap_i \mathfrak{q}_i$ is the primary decomposition, then, for any i, the radical of $\mathfrak{q}_i$ is an associated prime $\mathfrak{p}$ of $A/gA$ and so $f \in \phi^{-1}(\mathfrak{q}_i A_{\mathfrak{p}}) = \mathfrak{q}_i$ ; the equality here is because $\mathfrak{q}_i$ is a $\mathfrak{p}$ -primary ideal. Hence, the assertion holds.

Necessity

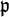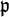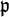Suppose A is a normal ring. For S₂, let $\mathfrak{p}$ be an associated prime of $A/fA$ for a non-zerodivisor f; we need to show it has height one. Replacing A by a localization, we can assume A is a local ring with maximal ideal $\mathfrak{p}$ . By definition, there is an element g in A such that $\mathfrak{p} = \{ x \in A | xg \equiv 0 \text{ mod }fA \}$ and $g \not\in fA$ . Put y = g/f in the total ring of fractions. If $y \mathfrak{p} \subset \mathfrak{p}$ , then $\mathfrak{p}$ is a faithful $A[y]$ -module and is a finitely generated A-module; consequently, $y$ is integral over A and thus in A, a contradiction. 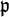Hence, $y \mathfrak{p} = A$ or $\mathfrak{p} = f/g A$ , which implies $\mathfrak{p}$ has height one (Krull's principal ideal theorem).

For R₁, we argue in the same way: let 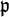$\mathfrak{p}$ be a prime ideal of height one. Localizing at 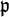$\mathfrak{p}$ we assume 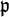$\mathfrak{p}$ is a maximal ideal and the similar argument as above shows that 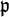$\mathfrak{p}$ is in fact principal. Thus, A is a regular local ring. $\square$

Notes

↑ EGA IV, § 5.7.

References

Grothendieck, Alexandre; Dieudonné, Jean (1965). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie". Publications Mathématiques de l'IHÉS 24. doi:10.1007/bf02684322. MR 0199181.
H. Matsumura, Commutative algebra, 1970.