Seriation (archaeology)

In archaeology, seriation is a relative dating method in which assemblages or artifacts from numerous sites, in the same culture, are placed in chronological order. Where absolute dating methods, such as carbon dating, cannot be applied, archaeologists have to use relative dating methods to date archaeological finds and features. Seriation is a standard method of dating in archaeology. It can be used to date stone tools, pottery fragments, and other artifacts. In Europe, it has been used frequently to reconstruct the chronological sequence of graves in a cemetery (e.g. Jørgensen 1992;[1] Müssemeier, Nieveler et al. 2003[2]).

Contextual and frequency seriation

Two different variants of seriation have been applied: contextual seriation and frequency seriation (Renfrew and Bahn 1996, pp. 116–117). Whereas contextual seriation is based on the presence or absence of a design style, frequency seriation relies on measuring the proportional abundance or frequency of a design style. Contextual seriation is often used for reconstructing the chronological sequence of graves as only the presence or absence of a design style or type is important. Frequency seriation is applied in case of large quantities of objects belonging to the same style. An example are assemblages of pottery sherds each including roughly the same range of types though in different proportions.

History

Flinders Petrie excavated at Diospolis Parva in Egypt in the late nineteenth century. He found that the graves he was uncovering contained no evidence of their dates and their discrete nature meant that a sequence could not be constructed through their stratigraphy. Petrie listed the contents of each grave on a strip of cardboard and swapped the papers around until he arrived at a sequence he was satisfied with.[3] He reasoned that the most accurate sequence would be the one where concentrations of certain design styles had the shortest duration across the sequence of papers (Renfrew and Bahn 1996, p. 116; Kendall 1971, p. 215; Shennan 1997, p. 341)[4]). Whereas Petrie is considered the inventor of contextual seriation, Bainerd (1951)[5] and Robinson (1951)[6] were the first to address the problem of frequency seriation (Shennan 1997, p. 342)[4]).

The model

Description of the model

The assumption that design styles follow a bell curve of popularity – starting slowly, growing to a peak and then dying away as another style becomes popular – provides the basis for frequency seriation. It also assumes that design popularity will be broadly similar from site to site within the same culture. In addition, it is vital that the lifespans of the different design styles overlap. Following these rules, an assemblage of objects can be placed into sequence so that sites with the most similar proportions of certain styles are always together (Lock 2003, p. 125).

Pitfalls

The task of identifying design styles i.e. to form groups of objects belonging to the same design style is by no means trivial. Creating a typology frequently is the basis of a seriation. Errors in typology result in errors in seriation: For example, if a certain design style had two peaks in popularity (bimodal distribution), this design style is not appropriate for seriation and its inclusion in the analysis may result in strange results. Some design styles were used for a very long time as the shape constructed was handy and no improvement or ornament was added. Of course, these design styles are not eligible for chronological seriation. For example, knives in early medieval times in Europe are said to show no chronological variation.

In addition to temporal organization, seriation results may reflect assemblage differences in social status, age, sex or those resulting from regional variation (or a combination of two or more of these factors). Shennan (1997, p. 343)[4] presents a seriation result of Danish hoards based on artefact types like daggers, axes, and swords. The result is not a chronological sequence due to the selection of types, the ordering seems to start with extremely male hoards and ends with extremely female ones.

Three conditions for chronological seriation

Doran and Hodson (1975, p. 269)[7] list three conditions that must be satisfied to obtain a chronological seriation result:

Statistical methods for seriation

Development of seriation methods

Nowadays, seriation results are no longer produced manually as in Petrie's times but by appropriate algorithms. Though according to David George Kendall (1971), Petrie's paper showed already a deep understanding of the mathematics of the seriation problem (Quote: "..in my view Petrie should be ranked with the greatest applied mathematicians of the nineteenth century"). In Baxter's (2003, p. 8) list of landmarks of statistics in archaeology the paper of Robinson (1951)[6] is the first entry. Robinson based his frequency seriation method on a similarity matrix. In 1971, Kendall proposed the use of multidimensional scaling techniques for seriation problems, and this approach has also been used by some other scientists (see Baxter 2003, pp. 202–203). Baxter also presents a review of statistical methods for seriation and a description of these approaches (pp. 202–207). In 1975, Doran and Hodson (pp. 269–281)[7] summarized the state of the art of seriation methods thoroughly, giving detailed descriptions of Kendall's and Robinson's approaches.

Correspondence analysis for seriation purposes

Today, the most popular seriation method both for contextual and frequency problems is based on correspondence analysis. The sequence of the first axis of a correspondence analysis is considered the best seriation order (Shennan 1997,[4] p. 342; Lock 2003, p. 127; Jensen & Høilund Nielsen 1997). Using this technique, not only the sequence of the objects but also those of the design styles is established. Note that external evidence is needed to establish the direction of the sequence calculated, i.e. the method does not tell whether the first object in the sequence is the oldest or the youngest object.

Kendall (1971) applied multidimensional scaling to the cemetery data of Münsingen. The resulting scatterplot showed the form of a horse-shoe where the graves were arranged on the curve according to their chronological order. Similarly, a mapping of the component scores for the first two axes of the correspondence analysis result will display a parabola if the design styles considered are controlled by one factor only (like chronology). This is called the arch effect by Hill and Gauch (1980).[8] Both Kendall and Jensen & Høilund Nielsen (1997) created artificial data sets to show that the parabola results in ideal circumstances. Therefore, it is recommended inspecting the scatterplot of the first two axes of correspondence analysis to find out if other factors play a role as well (see Examples 2 and 3).

If more than one factor is important, the arch effect may distort the results. Hill and Gauch (1980) presented a method to remove this effect.

In 2003, Groenen and Poblome adapted the correspondence analysis algorithm to combine seriation with absolute dates and stratigraphic relationships.[9][10]

Examples

Example 1: Small contextual seriation

The small example below was inspired by Flinders Petrie's serial ordering of Egyptian pottery as published by Renfrew and Bahn (1996, p. 117).

Raw data for contextual seriation
Result of contextual seriation


Another way of presenting the raw data for contextual seriation:
1=context contains the type
0=context does not contain the type

The raw data are stored in an unsorted binary contingency table indicating which design style can be found in which context by a star symbol. For example, consider the first column: context 3 contains the design styles blackrim, bottle, and handle. A beaker is contained in contexts 1 and 2. Contextual seriation sorts the design styles and the contexts in such a way that the star symbols are found as close as possible to the diagonal of the table. Of course, for a small examples like this, no computer programs are needed to find the best ordering, but for larger data sets like the 900 graves studied by Petrie they are extremely helpful.

Example 2: Simulated data, seriation and correspondence analysis

The data presented in this example was simulated by WinBasp. Initially 60 contexts (called units in WinBasp) were created along with 50 types. The contexts were labeled in chronological order by numbers 01 to 60, the types are labeled in the form T00001 to T00050. If a type is represented by one object only this object is not relevant for the chronological sequence as it does not provide a link to another context. Similarly, contexts containing one object only are irrelevant for seriation. Therefore, the contexts with one or no object and types represented by one object or not at all were eliminated. The resulting raw simulated data consisting of 43 contexts and 34 types are shown on the left. As expected, the dots indicating the occurrence of a type in a context are close to the diagonal of the table.

Raw simulated data for contextual seriation
Result of seriation


The image on the right hand side shows the result of the seriation for this data set. Note that the dots are even more compact along the diagonal of the table compared to the raw data. This shows a minor problem of seriation: In fact, the intervals of production may be somewhat longer than those calculated by the algorithm. In general, the sequences of contexts and types calculated by a seriation algorithm are not the correct chronological sequences but they are fairly close.

Result of correspondence analysis


The image above shows the scatterplot with the typical parabola shape of the first two axes of a correspondence analysis for the contexts of the simulated data set.

Example 3: Ideal data, seriation and correspondence analysis

Ideal seriation data

The contingency table shows 29 contexts with ideal seriation data as created by Kendall and Jensen & Høilund Nielsen (see above). With each new context a new type appears and another type disappears. For this regular data, it seems reasonable to assume constant time intervals for contexts adjacent in time.

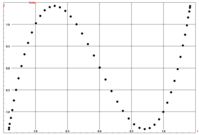
The correspondence analysis results shown in the figures below were calculated on the basis of 49 contexts with ideal seriation data. The scatterplot of the first two correspondence analysis axes shows the typical parabola shape. The display of the scores on the first and the third axes exhibits points lying on a third degree polynomial curve. Similarly, the plot of the scores on the first and the fourth axes will show a fourth degree polynomial for ideal data – and so on.

Note that the distances of the scores for adjacent contexts on the first axis vary: At the beginning and the end, the distances are extremely small, the largest distances in the centre is about 30 times as large as the smallest distance. Hill and Gauch (1979)[8] created a similar contingency table with a regular structure with each context containing six types. They note, too, that the within-context distances are smaller at the ends than in the middle. This was one of the reasons why they proposed an adjustment which is called detrended correspondence analysis.

Nevertheless, some archaeologists think that a linear transformation of the scores on the first axis on the basis of some known absolute dates will create good estimates for the unknown absolute dates, and this approach is the basis of the method presented by Groenen and Poblome (see above) to combine relative and absolute dates. This ideal example shows that a linear transformation might not be appropriate in all cases, though a simulation study by van de Velden, Groenen and Poblome comes to the conclusion that the predictions of the approach are quite good.[11]

Result of correspondence analysis: axes 1 and 2
Result of correspondence analysis: axes 1 and 3


See also

Notes

  1. ↑ Jørgensen, L. (ed.) (1992). Chronological Studies of Anglo-Saxon England, Lombard Italy and Vendel Period Sweden. Arkæologiske Skrifter 5. Copenhagen: Institute of Prehistoric and Classical Archaeology, University of Copenhagen. ISBN 87895000024 .
  2. ↑ Müssemeier, U., Nieveler, E., Plum, R., Pöppelmann, H. (2003). Chronologie der merowingerzeitlichen Grabfunde vom linken Niederrhein bis zur nördlichen Eifel. Materialien zur Bodendenkmalpflege im Rheinland, Heft 15. Köln: Rheinland-Verlag GmbH. ISBN 3-7927-1894-4.
  3. ↑ Petrie, F. W. M. (1899). Sequences in prehistoric remains. Journal of the Anthropological Institute 29:295–301
  4. ↑ 4.0 4.1 4.2 4.3 Shennan, St. (1997). Quantifying Archaeology. Edinburgh: Edinburgh University Press. ISBN 0-7486-0791-9.
  5. ↑ Brainerd, G.W. (1951). The place of chronological ordering in archaeological analysis. American Antiquity 16, pp.301–313
  6. ↑ 6.0 6.1 Robinson, W.S. (1951). A method for chronologically ordering archaeological deposits. American Antiquity 16, pp.293–301
  7. ↑ 7.0 7.1 Doran, J.E. and F.R. Hodson (1975). Mathematics and Computers in Archaeology. Edinburgh University Press. ISBN 0-85224-250-6.
  8. ↑ 8.0 8.1 Hill, M.O. and Gauch, H.G. (1980). Detrended Correspondence Analysis: An Improved Ordination Technique. Vegetatio 42, 47–58.
  9. ↑ Groenen, P. J. F. and J. Poblome (2003). Constrained correspondence analysis for seriation in archaeology applied to Sagalassos ceramic tablewares. In: Schwaiger, M. and O. Opitz (eds.), Exploratory Data Analysis in Empirical Research. Springer, Berlin: 90–97.
  10. ↑ Poblome, J. and P. J . F. Groenen (2003). Constrained correspondence analysis for seriation of Sagalassos tablewares. In M. Doerr and A. Sarris (eds.), Computer Applications and Quantitative Methods in Archaeology. Hellinic Ministry of Culture, 301–306.
  11. ↑ van de Velden, M., Groenen, P. J. F., Poblome, J. (2007). Seriation by constrained correspondence analysis: a simulation study. Econometric Institute Report EI 2007-40.

References

External links