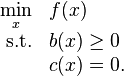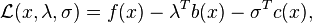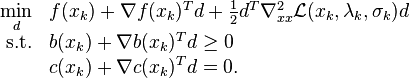Sequential quadratic programming
Sequential quadratic programming (SQP) is an iterative method for nonlinear optimization. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable.
SQP methods solve a sequence of optimization subproblems, each of which optimizes a quadratic model of the objective subject to a linearization of the constraints. If the problem is unconstrained, then the method reduces to Newton's method for finding a point where the gradient of the objective vanishes. If the problem has only equality constraints, then the method is equivalent to applying Newton's method to the first-order optimality conditions, or Karush–Kuhn–Tucker conditions, of the problem. SQP methods have been implemented in many packages, including NPSOL, SNOPT, NLPQL, OPSYC, OPTIMA, MATLAB, GNU Octave and SQP.
Algorithm basics
Consider a nonlinear programming problem of the form:
The Lagrangian for this problem is;
where 
and 
are Lagrange multipliers. At an iterate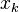 
, a basic sequential quadratic programming algorithm defines an appropriate search direction 
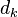as a solution to the quadratic programming subproblem
Note that the term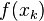 
in the expression above may be left out for the minimization problem, since it is constant.
See also
- Sequential linear programming
- Secant method
- Newton's method
References
- Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 3-540-35445-X. MR 2265882.
- Jorge Nocedal and Stephen J. Wright (2006). Numerical Optimization. Springer. ISBN 0-387-30303-0.
External links
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
