Separable space
In mathematics a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence 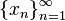 of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
Like the other axioms of countability, separability is a "limitation on size", not necessarily in terms of cardinality (though, in the presence of the Hausdorff axiom, this does turn out to be the case; see below) but in a more subtle topological sense. In particular, every continuous function on a separable space whose image is a subset of a Hausdorff space is determined by its values on the countable dense subset.
Contrast separability with the related notion of second countability, which is in general stronger but equivalent on the class of metrizable spaces.
First examples
Any topological space which is itself finite or countably infinite is separable, for the whole space is a countable dense subset of itself. An important example of an uncountable separable space is the real line, in which the rational numbers form a countable dense subset. Similarly the set of all vectors 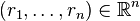 in which
in which 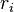 is rational for all i is a countable dense subset of
is rational for all i is a countable dense subset of 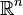 ; so for every
; so for every  the
the  -dimensional Euclidean space is separable.
-dimensional Euclidean space is separable.
A simple example of a space which is not separable is a discrete space of uncountable cardinality.
Further examples are given below.
Separability versus second countability
Any second-countable space is separable: if 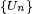 is a countable base, choosing any
is a countable base, choosing any  from the non-empty
from the non-empty 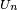 gives a countable dense subset. Conversely, a metrizable space is separable if and only if it is second countable, which is the case if and only if it is Lindelöf.
gives a countable dense subset. Conversely, a metrizable space is separable if and only if it is second countable, which is the case if and only if it is Lindelöf.
To further compare these two properties:
- An arbitrary subspace of a second countable space is second countable; subspaces of separable spaces need not be separable (see below).
- Any continuous image of a separable space is separable (Willard 1970, Th. 16.4a).; even a quotient of a second countable space need not be second countable.
- A product of at most countably many separable spaces is separable. A countable product of second countable spaces is second countable, but an uncountable product of second countable spaces need not even be first countable.
Cardinality
The property of separability does not in and of itself give any limitations on the cardinality of a topological space: any set endowed with the trivial topology is separable, as well as second countable, quasi-compact, and connected. The "trouble" with the trivial topology is its poor separation properties: its Kolmogorov quotient is the one-point space.
A first countable, separable Hausdorff space (in particular, a separable metric space) has at most the continuum cardinality  . In such a space, closure is determined by limits of sequences and any convergent sequence has at most one limit, so there is a surjective map from the set of convergent sequences with values in the countable dense subset to the points of
. In such a space, closure is determined by limits of sequences and any convergent sequence has at most one limit, so there is a surjective map from the set of convergent sequences with values in the countable dense subset to the points of  .
.
A separable Hausdorff space has cardinality at most 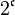 , where
, where  is the cardinality of the continuum. For this closure is characterized in terms of limits of filter bases: if
is the cardinality of the continuum. For this closure is characterized in terms of limits of filter bases: if 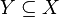 and
and 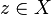 , then
, then  if and only if there exists a filter base
if and only if there exists a filter base 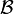 consisting of subsets of
consisting of subsets of  which converges to
which converges to 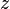 . The cardinality of the set
. The cardinality of the set 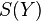 of such filter bases is at most
of such filter bases is at most  . Moreover, in a Hausdorff space, there is at most one limit to every filter base. Therefore, there is a surjection
. Moreover, in a Hausdorff space, there is at most one limit to every filter base. Therefore, there is a surjection  when
when 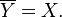
The same arguments establish a more general result: suppose that a Hausdorff topological space  contains a dense subset of cardinality
contains a dense subset of cardinality 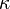 .
Then
.
Then  has cardinality at most
has cardinality at most 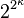 and cardinality at most
and cardinality at most 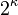 if it is first countable.
if it is first countable.
The product of at most continuum many separable spaces is a separable space (Willard 1970, p. 109, Th 16.4c). In particular the space 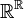 of all functions from the real line to itself, endowed with the product topology, is a separable Hausdorff space of cardinality
of all functions from the real line to itself, endowed with the product topology, is a separable Hausdorff space of cardinality 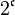 . More generally, if
. More generally, if 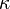 is any infinite cardinal, then a product of at most
is any infinite cardinal, then a product of at most  spaces with dense subsets of size at most
spaces with dense subsets of size at most 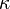 has itself a dense subset of size at most
has itself a dense subset of size at most 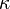 (Hewitt–Marczewski–Pondiczery theorem).
(Hewitt–Marczewski–Pondiczery theorem).
Constructive mathematics
Separability is especially important in numerical analysis and constructive mathematics, since many theorems that can be proved for nonseparable spaces have constructive proofs only for separable spaces. Such constructive proofs can be turned into algorithms for use in numerical analysis, and they are the only sorts of proofs acceptable in constructive analysis. A famous example of a theorem of this sort is the Hahn–Banach theorem.
Further examples
Separable spaces
- Every compact metric space (or metrizable space) is separable.
- The space
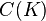 of all continuous functions from a compact subset
of all continuous functions from a compact subset 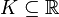 to the real line
to the real line 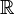 is separable.
is separable. - The Lebesgue spaces
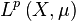 , over a separable measure space
, over a separable measure space 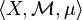 , are separable for any
, are separable for any 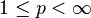 .
. - Any topological space which is the union of a countable number of separable subspaces is separable. Together, these first two examples give a different proof that
 -dimensional Euclidean space is separable.
-dimensional Euclidean space is separable. - The space
![C([0,1])](../I/m/8dbbcbb0e878bab88516ad2b7d27f8e0.png) of continuous real-valued functions on the unit interval
of continuous real-valued functions on the unit interval ![[0,1]](../I/m/ccfcd347d0bf65dc77afe01a3306a96b.png) with the metric of uniform convergence is a separable space, since it follows from the Weierstrass approximation theorem that the set
with the metric of uniform convergence is a separable space, since it follows from the Weierstrass approximation theorem that the set ![\mathbb{Q}[x]](../I/m/2e6941566cf570df9666c0d4d6480645.png) of polynomials in one variable with rational coefficients is a countable dense subset of
of polynomials in one variable with rational coefficients is a countable dense subset of ![C([0,1])](../I/m/8dbbcbb0e878bab88516ad2b7d27f8e0.png) . The Banach-Mazur theorem asserts that any separable Banach space is isometrically isomorphic to a closed linear subspace of
. The Banach-Mazur theorem asserts that any separable Banach space is isometrically isomorphic to a closed linear subspace of ![C([0,1])](../I/m/8dbbcbb0e878bab88516ad2b7d27f8e0.png) .
. - A Hilbert space is separable if and only if it has a countable orthonormal basis. It follows that any separable, infinite-dimensional Hilbert space is isometric to the space
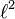 of square-summable sequences.
of square-summable sequences. - An example of a separable space that is not second-countable is the Sorgenfrey line
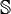 , the set of real numbers equipped with the lower limit topology.
, the set of real numbers equipped with the lower limit topology.
Non-separable spaces
- The first uncountable ordinal
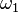 , equipped with its natural order topology, is not separable.
, equipped with its natural order topology, is not separable. - The Banach space
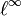 of all bounded real sequences, with the supremum norm, is not separable. The same holds for
of all bounded real sequences, with the supremum norm, is not separable. The same holds for 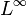 .
. - The Banach space of functions of bounded variation is not separable; note however that this space has very important applications in mathematics, physics and engineering.
Properties
- A subspace of a separable space need not be separable (see the Sorgenfrey plane and the Moore plane), but every open subspace of a separable space is separable, (Willard 1970, Th 16.4b). Also every subspace of a separable metric space is separable.
- In fact, every topological space is a subspace of a separable space of the same cardinality. A construction adding at most countably many points is given in (Sierpinski 1952, p. 49); if the space was a Hausdorff space then the space constructed which it embeds into is also a Hausdorff space.
- The set of all real-valued continuous functions on a separable space has a cardinality less than or equal to c. This follows since such functions are determined by their values on dense subsets.
- From the above property, one can deduce the following: If X is a separable space having an uncountable closed discrete subspace, then X cannot be normal. This shows that the Sorgenfrey plane is not normal.
- For a compact Hausdorff space X, the following are equivalent:
- (i) X is second countable.
- (ii) The space
 of continuous real-valued functions on X with the supremum norm is separable.
of continuous real-valued functions on X with the supremum norm is separable. - (iii) X is metrizable.
Embedding separable metric spaces
- Every separable metric space is homeomorphic to a subset of the Hilbert cube. This is established in the proof of the Urysohn metrization theorem.
- Every separable metric space is isometric to a subset of the (non-separable) Banach space l∞ of all bounded real sequences with the supremum norm; this is known as the Fréchet embedding. (Heinonen 2003)
- Every separable metric space is isometric to a subset of C([0,1]), the separable Banach space of continuous functions [0,1]→R, with the supremum norm. This is due to Stefan Banach. (Heinonen 2003)
- Every separable metric space is isometric to a subset of the Urysohn universal space.
For nonseparable spaces:
- A metric space of density equal to an infinite cardinal α is isometric to a subspace of C([0,1]α, R), the space of real continuous functions on the product of α copies of the unit interval. (Kleiber 1969)
References
- Heinonen, Juha (January 2003), Geometric embeddings of metric spaces (PDF), retrieved 6 February 2009
- Kelley, John L. (1975), General Topology, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90125-1, MR 0370454
- Kleiber, Martin; Pervin, William J. (1969), "A generalized Banach-Mazur theorem", Bull. Austral. Math. Soc. 1: 169–173, doi:10.1017/S0004972700041411
- Sierpiński, Wacław (1952), General topology, Mathematical Expositions, No. 7, Toronto, Ont.: University of Toronto Press, MR 0050870
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 507446
- Willard, Stephen (1970), General Topology, Addison-Wesley, ISBN 978-0-201-08707-9, MR 0264581