Separable sigma algebra
In mathematics, σ-algebras are usually studied in the context of measure theory. A separable σ-algebra (or separable σ-field) is a σ-algebra  which is a separable space when considered as a metric space with metric
which is a separable space when considered as a metric space with metric 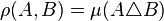 for
for 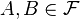 and a given measure
and a given measure  (and with
(and with 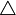 being the symmetric difference operator). Note that any σ-algebra generated by a countable collection of sets is separable, but the converse need not hold. For example, the Lebesgue σ-algebra is separable (since every Lebesgue measurable set is equivalent to some Borel set) but not countably generated (since its cardinality is higher than continuum).
being the symmetric difference operator). Note that any σ-algebra generated by a countable collection of sets is separable, but the converse need not hold. For example, the Lebesgue σ-algebra is separable (since every Lebesgue measurable set is equivalent to some Borel set) but not countably generated (since its cardinality is higher than continuum).
A separable measure space has a natural pseudometric that renders it separable as a pseudometric space. The distance between two sets is defined as the measure of the symmetric difference of the two sets. Note that the symmetric difference of two distinct sets can have measure zero; hence the pseudometric as defined above need not to be a true metric. However, if sets whose symmetric difference has measure zero are identified into a single equivalence class, the resulting quotient set can be properly metrized by the induced metric. If the measure space is separable, it can be shown that the corresponding metric space is, too.