Separable filter

A separable filter in image processing can be written as product of two more simple filters. Typically a 2-dimensional convolution operation is separated into 2 onedimensional filters. This reduces the cost of computing the operator.

Examples

1. A twodimensional smoothing filter is separated in this sample:

\frac{1}{3} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} * \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} = \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}

2. Gaussian blur (smoothing)

\frac{1}{4} \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix} * \frac{1}{4} \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} = \frac{1}{16} \begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix}

3. Sobel operator (edge detection)

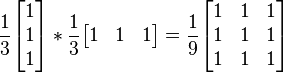
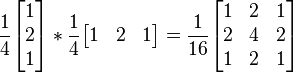
\mathbf{G_x} = \begin{bmatrix} \quad~ & \quad~ & \quad~ \\[-2.5ex] 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix} * A = \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix} * \begin{bmatrix} +1 & 0 & -1 \end{bmatrix} * A

This works also for Prewitt operator.