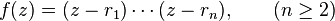Sendov's conjecture

In mathematics, Sendov's conjecture, sometimes also called Ilieff's conjecture, concerns the relationship between the locations of roots and critical points of a polynomial function of a complex variable. It is named after Blagovest Sendov.

The conjecture states that for a polynomial

f(z) = (z - r_1)\cdots (z-r_n),\qquad (n\ge 2)

with all roots r₁, ..., r_n inside the closed unit disk |z| ≤ 1, each of the n roots is at a distance no more than 1 from at least one critical point.

The Gauss–Lucas theorem says that all of the critical points lie within the convex hull of the roots. It follows that the critical points must be within the unit disk, since the roots are.

The conjecture has not been proved for n > 8. G. Schmieder announced a proof. .^[1]

History

This conjecture was first mooted by Blagovest Sendov in 1959. He propsoed this conjecture to Nikola Obreschkov. In 1967 this conjecture is misattributed to Ljubomir Iliev by Walter Hayman. In 1969 Mier and Sharmaad prove this conjecture for polynomials with n < 6. In 1991 Brown proves this conjecture for n < 7. Borcea extended the proof to n < 8 in 1996. Brown and Xiang proved the conjecture for n < 9 in 1999. Degot has proven this conjecture for large n but this proof requires additional conditions,

References

↑ Gerald Schmieder A proof of Sendov's conjecture

G. Schmeisser, "The Conjectures of Sendov and Smale," Approximation Theory: A Volume Dedicated to Blagovest Sendov (B. Bojoanov, ed.), Sofia: DARBA, 2002 pp. 353–369.

External links

Sendov's Conjecture by Bruce Torrence with contributions from Paul Abbott at The Wolfram Demonstrations Project