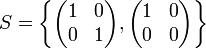In mathematics, a semigroup with two elements is a semigroup for which the cardinality of the underlying set is two. There are exactly five distinct nonisomorphic semigroups having two elements:
- O2, the null semigroup of order two,
- LO2 and RO2, the left zero semigroup of order two and right zero semigroup of order two, respectively,
- ({0,1}, ∧) (where "∧" is the logical connective "and"), or equivalently the set {0,1} under multiplication: the only semilattice with two elements and the only non-null semigroup with zero of order two, also a monoid, and ultimately the two-element Boolean algebra,
- (Z2, +2) (where Z2 = {0,1} and "+2" is "addition modulo 2"), or equivalently the set {−1,1} under multiplication: the only group of order two.
The semigroups LO2 and RO2 are antiisomorphic. O2, ({0,1}, ∧) and (Z2, +2) are commutative, LO2 and RO2 are noncommutative. LO2, RO2 and ({0,1}, ∧) are bands and also inverse semigroups.
Determination of semigroups with two elements
Choosing the set A = { 1, 2 } as the underlying set having two elements, sixteen binary operations can be defined in A. These operations are shown in the table below. In the table, a matrix of the form
indicates a binary operation on A having the following Cayley table.
List of binary operations in { 1, 2 }
|
|
|
|
|
| Null semigroup O2 |
≡ Semigroup ({0,1},  ) ) |
2·(1·2) = 2, (2·1)·2 = 1 |
Left zero semigroup LO2 |
|
|
|
|
|
| 2·(1·2) = 1, (2·1)·2 = 2 |
Right zero semigroup RO2 |
≡ Group (Z2, +2) |
≡ Semigroup ({0,1},  ) ) |
|
|
|
|
|
| 1·(1·2) = 2, (1·1)·2 = 1 |
≡ Group (Z2, +2) |
1·(1·1) = 1, (1·1)·1 = 2 |
1·(2·1) = 1, (1·2)·1 = 2 |
|
|
|
|
|
| 1·(1·1) = 2, (1·1)·1 = 1 |
1·(2·1) = 2, (1·2)·1 = 1 |
1·(1·2) = 2, (1·1)·2 = 1 |
Null semigroup O2 |
In this table:
- The semigroup ({0,1},
 ) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and pairing either with A creates a semigroup isomorphic to the semigroup ({0,1},
) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and pairing either with A creates a semigroup isomorphic to the semigroup ({0,1}, 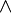 ). Every element is idempotent in this semigroup, so it is a band. Furthermore, it is commutative (abelian) and thus a semilattice. The order induced is a linear order, and so it is in fact a lattice and it is also a distributive and complemented lattice, i.e. it is actually the two-element Boolean algebra.
). Every element is idempotent in this semigroup, so it is a band. Furthermore, it is commutative (abelian) and thus a semilattice. The order induced is a linear order, and so it is in fact a lattice and it is also a distributive and complemented lattice, i.e. it is actually the two-element Boolean algebra.
- The two binary operations defined by matrices in a blue background are associative and pairing either with A creates a semigroup isomorphic to the null semigroup O2 with two elements.
- The binary operation defined by the matrix in an orange background is associative and pairing it with A creates a semigroup. This is the left zero semigroup LO2. It is not commutative.
- The binary operation defined by the matrix in a purple background is associative and pairing it with A creates a semigroup. This is the right zero semigroup RO2. It is also not commutative.
- The two binary operations defined by matrices in a red background are associative and pairing either with A creates a semigroup isomorphic to the group (Z2, +2).
- The remaining eight binary operations defined by matrices in a white background are not associative and hence none of them create a semigroup when paired with A.
The two-element semigroup ({0,1}, ∧)
The Cayley table for the semigroup ({0,1}, 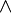 ) is given below:
) is given below:
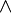 |
0 |
1 |
| 0 |
0 |
0 |
| 1 |
0 |
1 |
This is the simplest non-trivial example of a semigroup that is not a group. This semigroup has an identity element, 1, making it a monoid. It is also commutative. It is not a group because the element 0 does not have an inverse, and is not even a cancellative semigroup because we cannot cancel the 0 in the equation 1·0 = 0·0.
This semigroup arises in various contexts. For instance, if we choose 1 to be the truth value "true" and 0 to be the truth value "false" and the operation to be the logical connective "and", we obtain this semigroup in logic. It is isomorphic to the monoid {0,1} under multiplication. It is also isomorphic to the semigroup
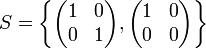
under matrix multiplication.[1]
The two-element semigroup (Z2,+2)
The Cayley table for the semigroup (Z2,+2) is given below:
This group is isomorphic to the cyclic group Z2 and the symmetric group S2.
Semigroups of order 3
Let A be the three-element set {1, 2, 3}. Altogether, a total of 39 = 19683 different binary operations can be defined on A. 113 of the 19683 binary operations determine 24 nonisomorphic semigroups, or 18 non-equivalent semigroups (with equivalence being isomorphism or anti-isomorphism).
[2] With the exception of the group with three elements, each of these has one (or more) of the above two-element semigroups as subsemigroups. [3] For example, the set {−1,0,1} under multiplication is a semigroup of order 3, and contains both {0,1} and {−1,1} as subsemigroups.
Finite semigroups of higher orders
Algorithms and computer programs have been developed for determining nonisomorphic finite semigroups of a given order. These have been applied to determine the nonisomorphic semigroups of small order.[3][4][5] The number of nonisomorphic semigroups with n elements, for n a nonnegative integer, is listed under  A027851 in the On-Line Encyclopedia of Integer Sequences.
A027851 in the On-Line Encyclopedia of Integer Sequences.  A001423 lists the number of non-equivalent semigroups, and
A001423 lists the number of non-equivalent semigroups, and  A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
See also
References
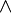 )
) 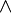 )
)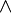 ) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and pairing either with A creates a semigroup isomorphic to the semigroup ({0,1},
) denotes the two-element semigroup containing the zero element 0 and the unit element 1. The two binary operations defined by matrices in a green background are associative and pairing either with A creates a semigroup isomorphic to the semigroup ({0,1}, 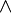 ). Every element is idempotent in this semigroup, so it is a band. Furthermore, it is commutative (abelian) and thus a semilattice. The order induced is a linear order, and so it is in fact a lattice and it is also a distributive and complemented lattice, i.e. it is actually the two-element Boolean algebra.
). Every element is idempotent in this semigroup, so it is a band. Furthermore, it is commutative (abelian) and thus a semilattice. The order induced is a linear order, and so it is in fact a lattice and it is also a distributive and complemented lattice, i.e. it is actually the two-element Boolean algebra. ) is given below:
) is given below:
![]() A027851 in the On-Line Encyclopedia of Integer Sequences.
A027851 in the On-Line Encyclopedia of Integer Sequences. ![]() A001423 lists the number of non-equivalent semigroups, and
A001423 lists the number of non-equivalent semigroups, and ![]() A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.
A023814 the number of associative binary operations, out of a total of nn2, determining a semigroup.