Semiconductor Bloch equations
The semiconductor Bloch equations[1] (abbreviated as SBEs) describe the optical response of semiconductors excited by coherent classical light sources, such as lasers. They are based on a full quantum theory, and form a closed set of integro-differential equations for the quantum dynamics of microscopic polarization and charge carrier distribution.[2][3] The SBEs are named after the structural analogy to the optical Bloch equations that describe the excitation dynamics in a two-level atom interacting with a classical electromagnetic field. As the major complication beyond the atomic approach, the SBEs must address the many-body interactions resulting from Coulomb force among charges and the coupling among lattice vibrations and electrons. The SBEs are one of the most sophisticated and successful approaches to describe optical properties of semiconductors originating from the classical light–matter interaction, once the many-body effects are systematically included.
Background
The optical response of a semiconductor follows if one can determine its macroscopic polarization 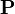 as a function of the electric field
as a function of the electric field 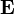 that excites it. The connection between
that excites it. The connection between 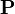 and the microscopic polarization
and the microscopic polarization  is given by
is given by
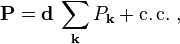
where the sum involves crystal-momenta 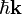 of all relevant electronic states. In semiconductor optics, one typically excites transitions between a valence and a conduction band. In this connection,
of all relevant electronic states. In semiconductor optics, one typically excites transitions between a valence and a conduction band. In this connection,  is the dipole matrix element between the conduction and valence band and
is the dipole matrix element between the conduction and valence band and 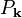 defines the corresponding transition amplitude.
defines the corresponding transition amplitude.
The derivation of the SBEs starts from a system Hamiltonian that fully includes the free-particles, Coulomb interaction, dipole interaction between classical light and electronic states, as well as the phonon contributions.[3] Like almost always in many-body physics, it is most convenient to apply the second-quantization formalism after the appropriate system Hamiltonian 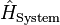 is identified. One can then derive the quantum dynamics of relevant observables
is identified. One can then derive the quantum dynamics of relevant observables 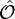 by using the Heisenberg equation of motion
by using the Heisenberg equation of motion
![\mathrm{i} \hbar \frac{\mathrm{d}}{\mathrm{d} t} \langle \hat{\mathcal{O}} \rangle
=
\langle [\hat{\mathcal{O}}, \hat{H}_{\mathrm{System}} ]_{-} \rangle\;.](../I/m/53535c2dceca3ad2466e22b56f485707.png)
Due to the many-body interactions within 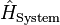 , the dynamics of the observable
, the dynamics of the observable 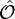 couples to new observables and the equation structure cannot be closed. This is the well-known BBGKY hierarchy problem that can be systematically truncated with different methods such as the cluster-expansion approach.[4]
couples to new observables and the equation structure cannot be closed. This is the well-known BBGKY hierarchy problem that can be systematically truncated with different methods such as the cluster-expansion approach.[4]
At operator level, the microscopic polarization is defined by an expectation value for a single electronic transition between a valence and a conduction band. In second quantization, conduction-band electrons are defined by fermionic creation and annihilation operators 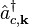 and
and 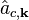 , respectively. An analogous identification, i.e.,
, respectively. An analogous identification, i.e., 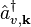 and
and 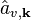 , is made for the valence band electrons. The corresponding electronic interband transition then becomes
, is made for the valence band electrons. The corresponding electronic interband transition then becomes

that describe transition amplitudes for moving an electron from conduction to valence band (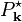 term) or vice versa (
term) or vice versa (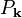 term). At the same time, an electron distribution follows from
term). At the same time, an electron distribution follows from
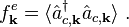
It is also convenient to follow the distribution of electronic vacancies, i.e., the holes,
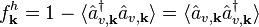
that are left to the valence band due to optical excitation processes.
Principal structure of SBEs
The quantum dynamics of optical excitations yields an integro-differential equations that constitute the SBEs[1][3]
Semiconductor Bloch equations ![\mathrm{i} \hbar \frac{\partial}{\partial t} P_{\mathbf{k}}
=
\tilde{\varepsilon}_{\mathbf{k}} P_{\mathbf{k}} - \left[ 1 - f^{e}_{\mathbf{k}}(t) - f^{h}_{\mathbf{k}}(t) \right] \Omega_{\mathbf{k}}
+ \mathrm{i} \hbar \left. \frac{\partial}{\partial t} P_{\mathbf{k}} \right|_{\mathrm{scatter}}\,,](../I/m/5a6e8e7d78cd751e61498c78674ef7cf.png)
![\hbar \frac{\partial}{\partial t} f^{e}_{\mathbf{k}}
=
2 \operatorname{Im} \left[ \Omega^\star_{\mathbf{k}} P_{\mathbf{k}} \right] + \hbar \left. \frac{\partial}{\partial t} f^{e}_{\mathbf{k}} \right|_{\mathrm{scatter}}\,,](../I/m/d43f6b20cfe40ccc3933e0dbf9110fec.png)
![\hbar \frac{\partial}{\partial t} f^{h}_{\mathbf{k}}
=
2 \operatorname{Im} \left[ \Omega^\star_{\mathbf{k}} P_{\mathbf{k}} \right] + \hbar \left. \frac{\partial}{\partial t} f^{h}_{\mathbf{k}} \right|_{\mathrm{scatter}}\;.](../I/m/80076e40998c36f300590fc2d15a1ea1.png)
These contain the renormalized Rabi energy
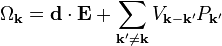
as well as the renormalized carrier energy
![\tilde{\varepsilon}_{\mathbf{k}}
=
\varepsilon_{\mathbf{k}}
- \sum_{\mathbf{k}' \neq \mathbf{k}} V_{\mathbf{k} - \mathbf{k}'} \left[ f^{e}_{\mathbf{k}'} + f^{h}_{\mathbf{k}'} \right]\,,](../I/m/7deae0ffc43c88271664225dd156cd9f.png)
where 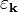 corresponds to the energy of free electron–hole pairs and
corresponds to the energy of free electron–hole pairs and 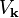 is the Coulomb matrix element, given here in terms of the carrier wave vector
is the Coulomb matrix element, given here in terms of the carrier wave vector 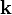 .
.
The symbolically denoted 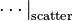 contributions stem from the hierarchical coupling due to many-body interactions. Conceptually,
contributions stem from the hierarchical coupling due to many-body interactions. Conceptually, 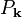 ,
, 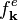 , and
, and 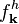 are single-particle expectation values while the hierarchical coupling originates from two-particle correlations such as polarization-density correlations or polarization-phonon correlations. Physically, these two-particle correlations introduce several nontrivial effects such as screening of Coulomb interaction, Boltzmann-type scattering of
are single-particle expectation values while the hierarchical coupling originates from two-particle correlations such as polarization-density correlations or polarization-phonon correlations. Physically, these two-particle correlations introduce several nontrivial effects such as screening of Coulomb interaction, Boltzmann-type scattering of 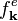 and
and 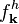 toward Fermi–Dirac distribution, excitation-induced dephasing, and further renormalization of energies due to correlations.
toward Fermi–Dirac distribution, excitation-induced dephasing, and further renormalization of energies due to correlations.
All these correlation effects can be systematically included by solving also the dynamics of two-particle correlations.[5] At this level of sophistication, one can use the SBEs to predict optical response of semiconductors without phenomenological parameters, which gives the SBEs a very high degree of predictability. Indeed, one can use the SBEs in order to predict suitable laser designs through the accurate knowledge they produce about the semiconductor's gain spectrum. One can even use the SBEs to deduce existence of correlations, such as bound excitons, from quantitative measurements.[6]
The presented SBEs are formulated in the momentum space since carrier's crystal momentum follows from 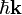 . An equivalent set of equations can also be formulated in position space.[7] However, especially, the correlation computations are much simpler to be performed in the momentum space.
. An equivalent set of equations can also be formulated in position space.[7] However, especially, the correlation computations are much simpler to be performed in the momentum space.
Interpretation and consequences
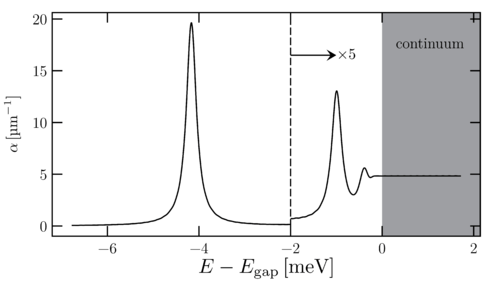
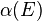 of bulk GaAs using two-band SBEs. The decay of polarization is approximated with a decay constant
of bulk GaAs using two-band SBEs. The decay of polarization is approximated with a decay constant 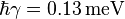 and
and 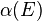 is computed as function of the pump field's photon energy
is computed as function of the pump field's photon energy  . The energy is shifted with respect to the band-gap energy
. The energy is shifted with respect to the band-gap energy 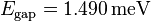 and the semiconductor is initially unexcited. Due to the small dephasing constant used, several excitonic resonances appear well below the bandgap energy. The magnitude of high-energy resonances are multiplied by 5 for visibility.
and the semiconductor is initially unexcited. Due to the small dephasing constant used, several excitonic resonances appear well below the bandgap energy. The magnitude of high-energy resonances are multiplied by 5 for visibility.The 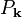 dynamic shows a structure where an individual
dynamic shows a structure where an individual 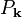 is coupled to all other microscopic polarizations due to the Coulomb interaction
is coupled to all other microscopic polarizations due to the Coulomb interaction 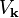 . Therefore, the transition amplitude
. Therefore, the transition amplitude 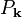 is collectively modified by the presence of other transition amplitudes. Only if one sets
is collectively modified by the presence of other transition amplitudes. Only if one sets 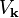 to zero, one finds isolated transitions within each
to zero, one finds isolated transitions within each 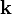 state that follow exactly the same dynamics as the optical Bloch equations predict. Therefore, already the Coulomb interaction among
state that follow exactly the same dynamics as the optical Bloch equations predict. Therefore, already the Coulomb interaction among 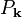 produces a new solid-state effect compared with optical transitions in simple atoms.
produces a new solid-state effect compared with optical transitions in simple atoms.
Conceptually, 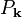 is just a transition amplitude for exciting an electron from valence to conduction band. At the same time, the homogeneous part of
is just a transition amplitude for exciting an electron from valence to conduction band. At the same time, the homogeneous part of 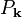 dynamics yields an eigenvalue problem that can be expressed through the generalized Wannier equation. Interestingly, the eigenstates of the Wannier equation is analogous to bound solutions of the hydrogen problem of quantum mechanics. These are often referred to as exciton solutions and they formally describe Coulombic binding by oppositely charged electrons and holes.
dynamics yields an eigenvalue problem that can be expressed through the generalized Wannier equation. Interestingly, the eigenstates of the Wannier equation is analogous to bound solutions of the hydrogen problem of quantum mechanics. These are often referred to as exciton solutions and they formally describe Coulombic binding by oppositely charged electrons and holes.
However, a real exciton is a true two-particle correlation because one must then have a correlation between one electron to another hole. Therefore, the appearance of exciton resonances in the polarization does not signify the presence of excitons because 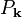 is a single-particle transition amplitude. The excitonic resonances are a direct consequence of Coulomb coupling among all transitions possible in the system. In other words, the single-particle transitions themselves are influenced by Coulomb interaction making it possible to detect exciton resonance in optical response even when true excitons are not present.[8]
is a single-particle transition amplitude. The excitonic resonances are a direct consequence of Coulomb coupling among all transitions possible in the system. In other words, the single-particle transitions themselves are influenced by Coulomb interaction making it possible to detect exciton resonance in optical response even when true excitons are not present.[8]
Therefore, it is often customary to specify optical resonances as excitonic instead of exciton resonances. The actual role of excitons on optical response can only be deduced by quantitative changes to induce to the linewidth and energy shift of excitonic resonances.[6]
The solutions of the Wannier equation can produces valuable insight to the basic properties of a semiconductor's optical response. In particular, one can solve the steady-state solutions of the SBEs to predict optical absorption spectrum analytically with the so-called Elliott formula. In this form, one can verify that an unexcited semiconductor shows several excitonic absorption resonances well below the fundamental bandgap energy. Obviously, this situation cannot be probing excitons because the initial many-body system does not contain electrons and holes to begin with. Furthermore, the probing can, in principle, be performed so gently that one essentially does not excite electron–hole pairs. This gedanken experiment illustrates nicely why one can detect excitonic resonances without having excitons in the system, all due to virtue of Coulomb coupling among transition amplitudes.
Extensions
The SBEs are particularly useful when solving the light propagation through a semiconductor structure. In this case, one needs to solve the SBEs together with the Maxwell's equations driven by the optical polarization. This self-consistent set is called the Maxwell–SBEs and is frequently applied to analyze present-day experiments and to simulate device designs.
At this level, the SBEs provide an extremely versatile method that describes linear as well as nonlinear phenomena such as excitonic effects, propagation effects, semiconductor microcavity effects, four-wave-mixing, polaritons in semiconductor microcavities, gain spectroscopy, and so on.[4][8][9] One can also generalize the SBEs by including excitation with terahertz (THz) fields[5] that are typically resonant with intraband transitions. One can also quantize the light field and investigate quantum-optical effects that result. In this situation, the SBEs become coupled to the semiconductor luminescence equations.
See also
- Absorption
- Semiconductor-luminescence equations
- Elliott formula
- Quantum-optical spectroscopy
- Optical Bloch equations
- Wannier equation
- Gain spectroscopy of semiconductors
- Semiconductor laser theory
Further reading
- Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics. Holt, Rinehart and Winston. ISBN 0-03-083993-9.
- Shah, J. (1999). Ultrafast Spectroscopy of Semiconductors and Semiconductor Nanostructures (2nd ed.). Springer. ISBN 978-3-540-64226-8.
- Kittel, C. (2004). Introduction to Solid State Physics (8th ed.). World Scientific. ISBN 047141526X.
- Haug, H.; Koch, S. W. (2009). Quantum Theory of the Optical and Electronic Properties of Semiconductors (5th ed.). World Scientific. ISBN 9812838848.
- Klingshirn, C. F. (2006). Semiconductor Optics. Springer. ISBN 978-3540383451.
- Kira, M.; Koch, S. W. (2011). Semiconductor Quantum Optics. Cambridge University Press. ISBN 978-0521875097.
References
- ↑ 1.0 1.1 Lindberg, M.; Koch, S. W. (1988). "Effective Bloch equations for semiconductors". Physical Review B 38 (5): 3342–3350. doi:10.1103%2FPhysRevB.38.3342
- ↑ Schäfer, W.; Wegener, M. (2002). Semiconductor Optics and Transport Phenomena. Springer. ISBN 3540616144.
- ↑ 3.0 3.1 3.2 Haug, H.; Koch, S. W. (2009). Quantum Theory of the Optical and Electronic Properties of Semiconductors (5th ed.). World Scientific. p. 216. ISBN 9812838848.
- ↑ 4.0 4.1 Kira, M.; Koch, S. W. (2011). Semiconductor Quantum Optics. Cambridge University Press. ISBN 978-0521875097.
- ↑ 5.0 5.1 Kira, M.; Koch, S.W. (2006). "Many-body correlations and excitonic effects in semiconductor spectroscopy". Progress in Quantum Electronics 30 (5): 155–296. doi:10.1016/j.pquantelec.2006.12.002
- ↑ 6.0 6.1 Smith, R. P.; Wahlstrand, J. K.; Funk, A. C.; Mirin, R. P.; Cundiff, S. T.; Steiner, J. T.; Schafer, M.; Kira, M. et al. (2010). "Extraction of Many-Body Configurations from Nonlinear Absorption in Semiconductor Quantum Wells". Physical Review Letters 104 (24). doi:10.1103/PhysRevLett.104.247401
- ↑ Stahl, A. (1984). "Electrodynamics of the band-edge in a direct gap semiconductor". Solid State Communications 49 (1): 91–93. doi:10.1016/0038-1098(84)90569-6
- ↑ 8.0 8.1 Koch, S. W.; Kira, M.; Khitrova, G.; Gibbs, H. M. (2006). "Semiconductor excitons in new light". Nature Materials 5 (7): 523–531. doi:10.1038/nmat1658
- ↑ Klingshirn, C. F. (2006). Semiconductor Optics. Springer. ISBN 978-3540383451.