Semi-Yao graph
The k-semi-Yao graph (k-SYG) of a set of n objects P is a geometric proximity graph, which was first described to present a kinetic data structure for maintenance of all the nearest neighbors on moving objects.[1] It is named for its relation to the Yao graph, which is named after Andrew Yao.
Construction
The k-SYG is constructed as follows. The space around each point p in P is partitioned into a set of polyhedral cones of opening angle 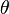 , meaning the angle of each pair of rays inside a polyhedral cone emanating from the apex is at most
, meaning the angle of each pair of rays inside a polyhedral cone emanating from the apex is at most 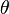 , and then p connects to k points of P in each of the polyhedral cones whose projections on the cone axis is minimum.
, and then p connects to k points of P in each of the polyhedral cones whose projections on the cone axis is minimum.
Properties
- The k-SYG, where k = 1, is known as the theta graph, and is the union of two Delaunay triangulations.[2]
- For a small
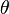 and an appropriate cone axis, the k-SYG gives a supergraph of the k-nearest neighbor graph (k-NNG).[3][4] For example, in 2D, if we partition the plane around each point into six wedges of equal angles, and pick the cone axes on directions of the cone bisectors, we obtain a k-SYG as a supergraph for the k-NNG.
and an appropriate cone axis, the k-SYG gives a supergraph of the k-nearest neighbor graph (k-NNG).[3][4] For example, in 2D, if we partition the plane around each point into six wedges of equal angles, and pick the cone axes on directions of the cone bisectors, we obtain a k-SYG as a supergraph for the k-NNG.
See also
References
- ↑ Rahmati, Zahed (2014). Simple, Faster Kinetic Data Structures (Thesis). University of Victoria.
- ↑ Bonichon, N.; Gavoille, C.; Hanusse, N.; Ilcinkas, D. (2010). "Connections between theta-graphs, Delaunay triangulations, and orthogonal surfaces". Graph Theoretic Concepts in Computer Science. pp. 266–278.
- ↑ Rahmati, Z.; Abam, M. A.; King, V.; Whitesides, S.; Zarei, A. (2015). "A simple, faster method for kinetic proximity problems". Computational Geometry 48 (4): 342–359.
- ↑ Rahmati, Z.; Abam, M. A.; King, V.; Whitesides, S. (2014). "Kinetic k-Semi-Yao Graph and its Applications". CoRR. abs/1412.5697.