Self-organized criticality
In physics, self-organized criticality (SOC) is a property of (classes of) dynamical systems that have a critical point as an attractor. Their macroscopic behaviour thus displays the spatial and/or temporal scale-invariance characteristic of the critical point of a phase transition, but without the need to tune control parameters to precise values.
The concept was put forward by Per Bak, Chao Tang and Kurt Wiesenfeld ("BTW") in a paper[1] published in 1987 in Physical Review Letters, and is considered to be one of the mechanisms by which complexity [2] arises in nature. Its concepts have been enthusiastically applied across fields as diverse as geophysics, physical cosmology, evolutionary biology and ecology, bio-inspired computing and optimization (mathematics), economics, quantum gravity, sociology, solar physics, plasma physics, neurobiology [3][4][5][6][7][8][9][10][11][12] [13] [14] [15] and others.
SOC is typically observed in slowly driven non-equilibrium systems with extended degrees of freedom and a high level of nonlinearity. Many individual examples have been identified since BTW's original paper, but to date there is no known set of general characteristics that guarantee a system will display SOC.
Overview
Self-organized criticality is one of a number of important discoveries made in statistical physics and related fields over the latter half of the 20th century, discoveries which relate particularly to the study of complexity in nature. For example, the study of cellular automata, from the early discoveries of Stanislaw Ulam and John von Neumann through to John Conway's Game of Life and the extensive work of Stephen Wolfram, made it clear that complexity could be generated as an emergent feature of extended systems with simple local interactions. Over a similar period of time, Benoît Mandelbrot's large body of work on fractals showed that much complexity in nature could be described by certain ubiquitous mathematical laws, while the extensive study of phase transitions carried out in the 1960s and 1970s showed how scale invariant phenomena such as fractals and power laws emerged at the critical point between phases. However, the term Self-Organized Criticality was firstly introduced by Bak, Tang and Wiesenfeld's 1987 paper which clearly linked together these factors: a simple cellular automaton was shown to produce several characteristic features observed in natural complexity (fractal geometry, pink (1/f) noise and power laws) in a way that could be linked to critical-point phenomena. Crucially, however, the paper emphasized that the complexity observed emerged in a robust manner that did not depend on finely tuned details of the system: variable parameters in the model could be changed widely without affecting the emergence of critical behaviour (hence, self-organized criticality). Thus, the key result of BTW's paper was its discovery of a mechanism by which the emergence of complexity from simple local interactions could be spontaneous — and therefore plausible as a source of natural complexity — rather than something that was only possible in the lab (or lab computer) where it was possible to tune control parameters to precise values. The publication of this research sparked considerable interest from both theoreticians and experimentalists, and important papers on the subject are among the most cited papers in the scientific literature.
Due to BTW's metaphorical visualization of their model as a "sandpile" on which new sand grains were being slowly sprinkled to cause "avalanches", much of the initial experimental work tended to focus on examining real avalanches in granular matter, the most famous and extensive such study probably being the Oslo ricepile experiment. Other experiments include those carried out on magnetic-domain patterns, the Barkhausen effect and vortices in superconductors. Early theoretical work included the development of a variety of alternative SOC-generating dynamics distinct from the BTW model, attempts to prove model properties analytically (including calculating the critical exponents[16][17]), and examination of the necessary conditions for SOC to emerge. One of the important issues for the latter investigation was whether conservation of energy was required in the local dynamical exchanges of models: the answer in general is no, but with (minor) reservations, as some exchange dynamics (such as those of BTW) do require local conservation at least on average. In the long term, key theoretical issues yet to be resolved include the calculation of the possible universality classes of SOC behaviour and the question of whether it is possible to derive a general rule for determining if an arbitrary algorithm displays SOC.
Alongside these largely lab-based approaches, many other investigations have centered around large-scale natural or social systems that are known (or suspected) to display scale-invariant behavior. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including: earthquakes (which, long before SOC was discovered, were known as a source of scale-invariant behavior such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes and the Omori law describing the frequency of aftershocks, and where models that displayed SOC were proposed and analyzed prior to the BTW 87 paper;[3][4]); solar flares; fluctuations in economic systems such as financial markets (references to SOC are common in econophysics); landscape formation; forest fires; landslides; epidemics; neuronal avalanches in cortex;[6][11] 1/f noise in the amplitude envelope of electrophysiological signals;[5] and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). These "applied" investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.
The recent excitement generated by scale-free networks has raised some interesting new questions for SOC-related research: a number of different SOC models have been shown to generate such networks as an emergent phenomenon, as opposed to the simpler models proposed by network researchers where the network tends to be assumed to exist independently of any physical space or dynamics.
Despite the considerable interest and research output generated from the SOC hypothesis there remains no general agreement with regards to its mathematical mechanisms. Bak Tang and Wiesenfeld based their hypothesis on the behavior of their sandpile model.[1] However, this model was subsequently shown to actually generate 1/f2 noise rather than 1/f noise.[18] Other simulation models were proposed later that could produce true 1/f noise,[19] And, experimental sandpile models were observed to yield 1/f noise.[20]
In addition to the nonconservative theoretical model mentioned above, other theoretical models for SOC have been based upon information theory[21] and mean field theory,[22] but no particular model explaining SOC has found general acceptance.
Alternatively, a mathematical model that appears to fully explain 1/f noise and other power law phenomena associated with SOC has been proposed on the basis of the mathematical properties of certain error distributions of the generalized linear model.[23] The behavior of these error distributions lends itself to description by exponential dispersion models characterized by mathematical closure under additive and reproductive convolution as well as under scale transformations: These models, known as the Tweedie distributions, are further characterized by an inherent variance to mean power law. More critically, the Tweedie distributions act as foci of mathematical convergence in a mathematical limit theorem[24] for a wide range of statistical processes, much as how the Gaussian distribution serves as a focus of mathematical convergence in the central limit theorem.
Consequent to this limit theorem we find an alternative paradigm to mechanistically explain phenomena attributed to SOC that becomes framed on the statistical theory of errors rather than the behavior of dynamical systems. The premises of criticality, absence of fine-tuning and self-organization, on which the hypothesis of SOC is based, would be replaced by a mathematical convergence theorem and the transformational properties of these Tweedie exponential dispersion models, offering a possible paradigm shift in the understanding of 1/f noise and related power law phenomena.
Examples of self-organized critical dynamics
In chronological order of development:
See also
- 1/f noise
- Complex systems
- Detrended fluctuation analysis, a method to detect power-law scaling in time series.
- Fractals
- Power laws
- Scale invariance
- Self-organization
- Critical exponents
- Ilya Prigogine, a systems scientist who helped formalize dissipative system behavior in general terms.
- Red Queen hypothesis
- Self-organized criticality control
References
- ↑ 1.0 1.1 Bak, P., Tang, C. and Wiesenfeld, K. (1987). "Self-organized criticality: an explanation of 1/f noise". Physical Review Letters 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. Papercore summary: http://papercore.org/Bak1987.
- ↑ Bak, P., and Paczuski, M. (1995). "Complexity, contingency, and criticality". Proc Natl Acad Sci U S A. 92 (15): 6689–6696. Bibcode:1995PNAS...92.6689B. doi:10.1073/pnas.92.15.6689. PMC 41396. PMID 11607561.
- ↑ 3.0 3.1 Turcotte, D. L.; Smalley, R. F., Jr.; Solla, S. A. (1985). "Collapse of loaded fractal trees". Nature 313 (6004): 671. Bibcode:1985Natur.313..671T. doi:10.1038/313671a0.
- ↑ 4.0 4.1 Smalley, R. F., Jr.; Turcotte, D. L.; Solla, S. A. (1985). "A renormalization group approach to the stick-slip behavior of faults". Journal of Geophysical Research 90 (B2): 1894. Bibcode:1985JGR....90.1894S. doi:10.1029/JB090iB02p01894.
- ↑ 5.0 5.1 K. Linkenkaer-Hansen, V. V. Nikouline, J. M. Palva, and R. J. Ilmoniemi. (2001). "Long-Range Temporal Correlations and Scaling Behavior in Human Brain Oscillations". J. Neurosci. 21 (4): 1370–1377. PMID 11160408.
- ↑ 6.0 6.1 J. M. Beggs and D. Plenz (2006). "Neuronal Avalanches in Neocortical Circuits". J. Neurosci 23.
- ↑ Chialvo, D. R. (2004). "Critical brain networks". Physica A 340 (4): 756–765. arXiv:cond-mat/0402538. Bibcode:2004PhyA..340..756C. doi:10.1016/j.physa.2004.05.064.
- ↑ Stefan Boettcher (1999). "Extremal optimization of graph partitioning at the percolation threshold". J. Phys. A: Math. Gen 32 (28): 5201–5211. arXiv:cond-mat/9901353. Bibcode:1999JPhA...32.5201B. doi:10.1088/0305-4470/32/28/302.
- ↑ D. Fraiman, P. Balenzuela, J. Foss and D. R. Chialvo (2004). "Ising-like dynamics in large scale brain functional networks". Physical Review E 79 (6): 061922. arXiv:0811.3721. Bibcode:2009PhRvE..79f1922F. doi:10.1103/PhysRevE.79.061922.
- ↑ L. de Arcangelis, C. Perrone-Capano, and H. J. Herrmann (2006). "Self-organized criticality model for brain plasticity". Phys. Rev. Lett. 96. doi:10.1103/physrevlett.96.028107.
- ↑ 11.0 11.1 Poil, SS; Hardstone, R; Mansvelder, HD; Linkenkaer-Hansen, K (Jul 2012). "Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks". Journal of Neuroscience 32 (29): 9817–23. doi:10.1523/JNEUROSCI.5990-11. PMC 3553543. PMID 22815496.
- ↑ Manfred G. Kitzbichler, Marie L. Smith, Søren R. Christensen, Ed Bullmore1 (2009). Behrens, Tim, ed. "Broadband Criticality of Human Brain Network Synchronization". PLoS Comput Biol 5 (3): e1000314. doi:10.1371/journal.pcbi.1000314. PMC 2647739. PMID 19300473.
- ↑ Chialvo, D. R. (2010). "Emergent complex neural dynamics". Nature Physics 6: 744–750. arXiv:1010.2530. Bibcode:2010NatPh...6..744C. doi:10.1038/nphys1803.
- ↑ Tagliazucchi E, Balenzuela P, Fraiman D and Chialvo DR. (2012). "Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis". Front. Physiol. 3: 15. doi:10.3389/fphys.2012.00015.
- ↑ Haimovici A, Tagliazucchi E, Balenzuela P and Chialvo DR. (2013). "Brain Organization into Resting State Networks Emerges at Criticality on a Model of the Human Connectome". Physical Review Letters 110: 178101. arXiv:1209.5353. Bibcode:2013PhRvL.110q8101H. doi:10.1103/PhysRevLett.110.178101.
- ↑ Tang, C. and Bak, P. (1988). "Critical exponents and scaling relations for self-organized critical phenomena". Physical Review Letters 60 (23): 2347–2350. doi:10.1103/PhysRevLett.60.2347.
- ↑ Tang, C. and Bak, P. (1988). "Mean field theory of self-organized critical phenomena". Journal of Statistical Physics 51 (5-6): 797–802. doi:10.1007/BF01014884.
- ↑ Jensen, H. J., Christensen, K. and Fogedby, H. C. (1989). "1/f noise, distribution of lifetimes, and a pile of sand". Phys. Rev. B 40: 7425. doi:10.1103/physrevb.40.7425.
- ↑ Maslov, S., Tang, C. and Zhang, Y. - C. (1999). "1/f noise in Bak-Tang-Wiesenfeld models on narrow stripes". Phys. Rev. Lett. 83: 2449. doi:10.1103/physrevlett.83.2449.
- ↑ Frette, V., Christinasen, K., Malthe-Sørenssen,A., Feder, J, Jøssang, T and Meaken, P (1996). "Avalanche dynamics in a pile of rice". Nature 379: 49. doi:10.1038/379049a0.
- ↑ Dewar, R. (2003). "Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states". J. Phys. A: Math. Gen. 36: 631–641. doi:10.1088/0305-4470/36/3/303.
- ↑ Vespignani, A., and Zapperi,S. (1998). "How self-organized criticality works: a unified mean-field picture". Phys. Rev. E 57: 6345. doi:10.1103/physreve.57.6345.
- ↑ Kendal, W. (2015). "Self-organized criticality attributed to a central limit-like convergence effect". Physica A 421: 141–150. doi:10.1016/j.physa.2014.11.035.
- ↑ Jørgensen, B; Martinez, JR & Tsao, M (1994). "Asymptotic behaviour of the variance function". Scand J Statist 21: 223–243.
Further reading
- An overview of self-organized criticality with many references
- Adami, C. (1995). "Self-organized criticality in living systems". Physics Letters A 203 (1): 29–32. Bibcode:1995PhLA..203...29A. doi:10.1016/0375-9601(95)00372-A.
- Bak, P. (1996). How Nature Works: The Science of Self-Organized Criticality. New York: Copernicus. ISBN 0-387-94791-4.
- Bak, P. and Paczuski, M. (1995). "Complexity, contingency, and criticality". Proceedings of the National Academy of Sciences of the USA 92 (15): 6689–6696. Bibcode:1995PNAS...92.6689B. doi:10.1073/pnas.92.15.6689. PMC 41396. PMID 11607561.
- Bak, P. and Sneppen, K. (1993). "Punctuated equilibrium and criticality in a simple model of evolution". Physical Review Letters 71 (24): 4083–4086. Bibcode:1993PhRvL..71.4083B. doi:10.1103/PhysRevLett.71.4083. PMID 10055149.
- Bak, P., Tang, C. and Wiesenfeld, K. (1987). "Self-organized criticality: an explanation of
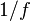 noise". Physical Review Letters 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381.
noise". Physical Review Letters 59 (4): 381–384. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381.
- Bak, P., Tang, C. and Wiesenfeld, K. (1988). "Self-organized criticality". Physical Review A 38 (1): 364–374. Bibcode:1988PhRvA..38..364B. doi:10.1103/PhysRevA.38.364. Papercore summary.
- Buchanan, M. (2000). Ubiquity. London: Weidenfeld & Nicolson. ISBN 0-7538-1297-5.
- Jensen, H. J. (1998). Self-Organized Criticality. Cambridge: Cambridge University Press. ISBN 0-521-48371-9.
- Katz, J. I. (1986). "A model of propagating brittle failure in heterogeneous media". Journal of Geophysical Research 91 (B10): 10412. Bibcode:1986JGR....9110412K. doi:10.1029/JB091iB10p10412.
- Kron, T./Grund, T. (2009). "Society as a Selforganized Critical System". Cybernetics and Human Knowing 16: 65–82.
- Paczuski, M. (2005). "Networks as renormalized models for emergent behavior in physical systems". The Science and Culture Series – Physics. arXiv:physics/0502028. Bibcode:2005cmn..conf..363P. doi:10.1142/9789812701558_0042. ISBN 978-981-256-525-9.
- Turcotte, D. L. (1997). Fractals and Chaos in Geology and Geophysics. Cambridge: Cambridge University Press. ISBN 0-521-56733-5.
- Turcotte, D. L. (1999). "Self-organized criticality". Reports on Progress in Physics 62 (10): 1377–1429. Bibcode:1999RPPh...62.1377T. doi:10.1088/0034-4885/62/10/201.
- Md. Nurujjaman/A. N. Sekar Iyengar (2007). "Realization of {SOC} behavior in a dc glow discharge plasma". Physics Letters A 360: 717–721. arXiv:physics/0611069. Bibcode:2007PhLA..360..717N. doi:10.1016/j.physleta.2006.09.005.