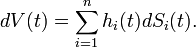Self-financing portfolio
A self-financing portfolio is an important concept in financial mathematics.
A portfolio is self-financing if there is no exogenous infusion or withdrawal of money; the purchase of a new asset must be financed by the sale of an old one.
Mathematical definition
Let 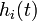 denote the number of stock number 'i' in the portfolio at time
denote the number of stock number 'i' in the portfolio at time  , and
, and 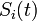 the price of stock number 'i' in a frictionless market with trading in continuous time. Let
the price of stock number 'i' in a frictionless market with trading in continuous time. Let

Then the portfolio  is self-financing if
is self-financing if
Discrete time
Assume we are given a discrete filtered probability space 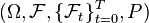 , and let
, and let 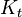 be the solvency cone (with or without transaction costs) at time t for the market. Denote by
be the solvency cone (with or without transaction costs) at time t for the market. Denote by  . Then a portfolio
. Then a portfolio 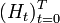 (in physical units, i.e. the number of each stock) is self-financing (with trading on a finite set of times only) if
(in physical units, i.e. the number of each stock) is self-financing (with trading on a finite set of times only) if
- for all
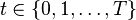 we have that
we have that 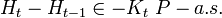 with the convention that
with the convention that  .[2]
.[2]
If we are only concerned with the set that the portfolio can be at some future time then we can say that 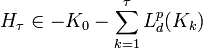 .
.
If there are transaction costs then only discrete trading should be considered, and in continuous time then the above calculations should be taken to the limit such that 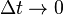 .
.
See also
References
- ↑ Björk, Tomas (2009). Arbitrage theory in continuous time (3rd ed.). Oxford University Press. p. 87. ISBN 978-0-19-877518-8.
- ↑ Hamel, Andreas; Heyde, Frank; Rudloff, Birgit (November 30, 2010). "Set-valued risk measures for conical market models" (pdf). Retrieved February 2, 2011.