Seiberg–Witten theory

For applications to 4-manifolds see Seiberg–Witten invariant

In theoretical physics, Seiberg–Witten theory is a theory that determines an exact low-energy effective action (for massless degrees of freedom) of a N=2 supersymmetric gauge theory—namely the metric of the moduli space of vacua.

Seiberg-Witten curves

In general, effective Lagrangians of supersymmetric gauge theories are largely determined by their holomorphic properties and their behavior near the singularities. In particular, in gauge theory with N = 2 extended supersymmetry, the moduli space of vacua is a special Kähler manifold and its Kähler potential is constrained by above conditions.

In the original derivation by Seiberg and Witten, they extensively used holomorphy and electric-magnetic duality to constrain the prepotential, namely the metric of the moduli space of vacua.

Consider the example with gauge group SU(n).The classical potential is:

V(x) = \frac{1}{g^2} \operatorname{Tr} [\phi , \bar{\phi} ]^2 \,

 

 

 

 

(1)

This must vanish on the moduli space, so vacuum expectation value of φ can be gauge rotated into Cartan subalgebra, so it is a traceless diagonal complex matrix.

Because the fields φ no longer have vanishing Vacuum expectation value. Because these are now heavy due to the Higgs effect, they should be integrated out in order to find the effective N=2 Abelian gauge theory. This can be expressed in terms of a single holomorphic function F.

In terms of this prepotential the Lagrangian can be written in the form:

\frac{1}{4\pi} \operatorname{Im} \Bigl[ \int d^4 \theta \frac{dF}{dA} \bar{A} + \int d^2 \theta \frac{1}{2} \frac{d^2 F}{dA^2} W_\alpha W^\alpha \Bigr] \,

 

 

 

 

(3)

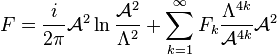
F = \frac{i}{2\pi} \mathcal{A}^2 \operatorname{\ln}\frac{\mathcal{A}^2}{\Lambda^2} + \sum_{k=1}^\infty F_k \frac{\Lambda^{4k}}{\mathcal{A}^{4k}} \mathcal{A}^2 \,

 

 

 

 

(4)

The first term is a perturbative loop calculation and the second is the instanton part where k labels fixed instanton numbers.

From this we can get the mass of the BPS particles.

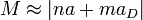
M \approx |na+ma_D| \,

 

 

 

 

(5)

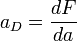
a_D = \frac{dF}{da} \,

 

 

 

 

(6)

One way to interpret this is that these variables a and its dual can be expressed as periods of a meromorphic differential on a Riemann surface called the Seiberg-Witten curve.

Seiberg-Witten prepotential via instanton counting

Consider a super Yang-Mills theory in curved 6-dimensional background. After dimensional reduction on 2-torus, we obtain a 4d N = 2 super Yang-Mills theory with additional terms. Turning Wilson lines to compensate holonomies of fermions on the 2-torus, we get 4d N = 2 SYM in　Ω-background. Ω has 2 parameters, ε1,ε2, which go to 0 in the flat limit.

In Ω-background, we can integrate out all the non-zero modes, so the partition function (with the boundary condition φ → 0 at x → ∞) can be expressed as a sum of products and ratios of fermionic and bosonic determinants over instanton number. In the limit where ε1,ε2 approach 0, this sum is dominated by a unique saddle point. On the other hand, when ε1,ε2 approach 0,

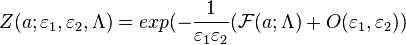
Z(a;\varepsilon_{1},\varepsilon_{2},\Lambda)=exp(-\frac{1}{\varepsilon_{1}\varepsilon_{2}}(\mathcal{F}(a;\Lambda)+O(\varepsilon_{1},\varepsilon_{2}))\,

 

 

 

 

(10)

holds.

See also

External links