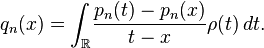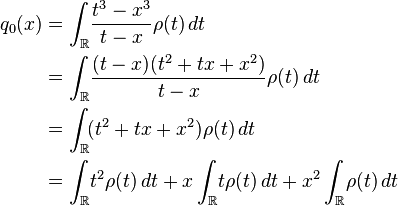Secondary polynomials

In mathematics, the secondary polynomials 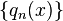$\{q_n(x)\}$ associated with a sequence 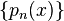$\{p_n(x)\}$ of polynomials orthogonal with respect to a density 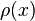$\rho(x)$ are defined by

q_n(x) = \int_\mathbb{R}\! \frac{p_n(t) - p_n(x)}{t - x} \rho(t)\,dt.

To see that the functions 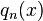$q_n(x)$ are indeed polynomials, consider the simple example of 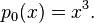$p_0(x)=x^3.$ Then,

\begin{align} q_0(x) &{} = \int_\mathbb{R} \! \frac{t^3 - x^3}{t - x} \rho(t)\,dt \\ &{} = \int_\mathbb{R} \! \frac{(t - x)(t^2+tx+x^2)}{t - x} \rho(t)\,dt \\ &{} = \int_\mathbb{R} \! (t^2+tx+x^2)\rho(t)\,dt \\ &{} = \int_\mathbb{R} \! t^2\rho(t)\,dt + x\int_\mathbb{R} \! t\rho(t)\,dt + x^2\int_\mathbb{R} \! \rho(t)\,dt \end{align}

which is a polynomial $x$ provided that the three integrals in $t$ (the moments of the density $\rho$ ) are convergent.

Secondary polynomials

See also