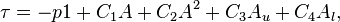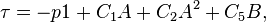Second-order fluid

A second-order fluid is a fluid where the stress tensor is the sum of all tensors that can be formed from the velocity field with up to two derivatives. So that the total stress tensor can be written

\tau = -p 1 + C_1 A + C_2 A^2 + C_3 A_u + C_4 A_l,

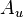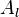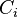where $A$ is the strain tensor, $A_u$ is the upper convected derivative of $A$ and $A_l$ is the lower convected derivative of $A$ . The coefficients $C_i$ are functions of the tensor invariants of $A$ . An Euler fluid is a zeroth order fluid and a Newtonian fluid is a first order one.

For a steady flow this can be written

\tau = -p 1 + C_1 A + C_2 A^2 + C_5 B,

where B is the second Rivlin-Ericksen tensor, and 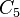$C_5$ is a new constant.

References

Bird, RB., Armstrong, RC., Hassager, O., Dynamics of Polymeric Liquids: Second Edition, Volume 1: Fluid Mechanics. John Wiley and Sons 1987 ISBN 047180245X(v.1)

Bird R.B, Stewart W.E, Light Foot E.N.: Transport phenomena, John Wiley and Sons, Inc. New York, U.S.A., 1960