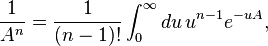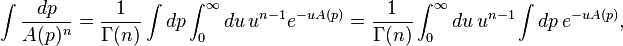Schwinger parametrization
Schwinger parametrization is a technique for evaluating loop integrals which arise from Feynman diagrams with one or more loops.
Using the well-known observation that
Julian Schwinger noticed that one may simplify the integral:
for Re(n)>0.
Another version of Schwinger parametrization is:
and it is easy to generalize this identity to n denominators.
See also Feynman parametrization.