Schwarz–Ahlfors–Pick theorem
In mathematics, the Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma for hyperbolic geometry, such as the Poincaré half-plane model.
The Schwarz–Pick lemma states that every holomorphic function from the unit disk U to itself, or from the upper half-plane H to itself, will not increase the Poincaré distance between points. The unit disk U with the Poincaré metric has negative Gaussian curvature −1. In 1938, Lars Ahlfors generalised the lemma to maps from the unit disk to other negatively curved surfaces:
Theorem (Schwarz–Ahlfors–Pick). Let U be the unit disk with Poincaré metric  ; let S be a Riemann surface endowed with a Hermitian metric
; let S be a Riemann surface endowed with a Hermitian metric  whose Gaussian curvature is ≤ −1; let
whose Gaussian curvature is ≤ −1; let 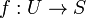 be a holomorphic function. Then
be a holomorphic function. Then
for all 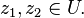
A generalization of this theorem was proved by Shing-Tung Yau in 1973.[1]
References
- ↑ Robert Osserman (September 1999). "From Schwarz to Pick to Ahlfors and Beyond". Notices of the AMS.