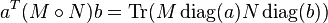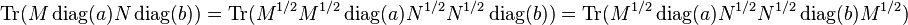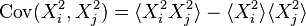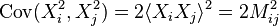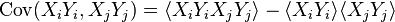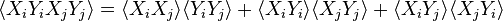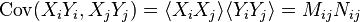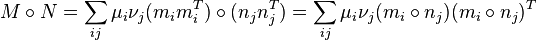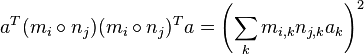Schur product theorem
In mathematics, particularly in linear algebra, the Schur product theorem states that the Hadamard product of two positive definite matrices is also a positive definite matrix. The result is named after Issai Schur[1] (Schur 1911, p. 14, Theorem VII) (note that Schur signed as J. Schur in Journal für die reine und angewandte Mathematik.[2][3])
Proof
Proof using the trace formula
It is easy to show that for matrices  and
and  , the Hadamard product
, the Hadamard product 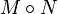 considered as a bilinear form acts on vectors
considered as a bilinear form acts on vectors  as
as
where 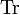 is the matrix trace and
is the matrix trace and 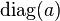 is the diagonal matrix having as diagonal entries the elements of
is the diagonal matrix having as diagonal entries the elements of  .
.
Since  and
and  are positive definite, we can consider their square-roots
are positive definite, we can consider their square-roots 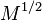 and
and 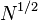 and write
and write
Then, for 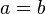 , this is written as
, this is written as 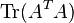 for
for 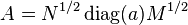 and thus is positive. This shows that
and thus is positive. This shows that 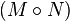 is a positive definite matrix.
is a positive definite matrix.
Proof using Gaussian integration
Case of M = N
Let  be an
be an  -dimensional centered Gaussian random variable with covariance
-dimensional centered Gaussian random variable with covariance 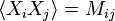 .
Then the covariance matrix of
.
Then the covariance matrix of 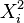 and
and 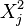 is
is
Using Wick's theorem to develop 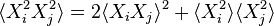 we have
we have
Since a covariance matrix is positive definite, this proves that the matrix with elements 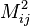 is a positive definite matrix.
is a positive definite matrix.
General case
Let  and
and  be
be  -dimensional centered Gaussian random variables with covariances
-dimensional centered Gaussian random variables with covariances 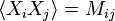 ,
, 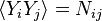 and independt from each other so that we have
and independt from each other so that we have
-
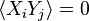 for any
for any 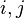
Then the covariance matrix of 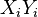 and
and 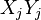 is
is
Using Wick's theorem to develop
and also using the independence of  and
and  , we have
, we have
Since a covariance matrix is positive definite, this proves that the matrix with elements 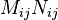 is a positive definite matrix.
is a positive definite matrix.
Proof using eigendecomposition
Proof of positivity
Let 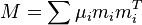 and
and 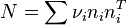 . Then
. Then
Each 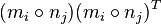 is positive (but, except in the 1-dimensional case, not positive definite, since they are rank 1 matrices) and
is positive (but, except in the 1-dimensional case, not positive definite, since they are rank 1 matrices) and 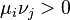 , thus the sum giving
, thus the sum giving 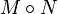 is also positive.
is also positive.
Complete proof
To show that the result is positive definite requires further proof. We shall show that for any vector 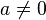 , we have
, we have 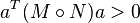 . Continuing as above, each
. Continuing as above, each 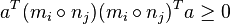 , so it remains to show that there exist
, so it remains to show that there exist  and
and 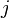 for which the inequality is strict. For this we observe that
for which the inequality is strict. For this we observe that
Since  is positive definite, there is a
is positive definite, there is a 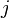 for which
for which 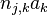 is not 0 for all
is not 0 for all  , and then, since
, and then, since  is positive definite, there is an
is positive definite, there is an  for which
for which 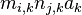 is not 0 for all
is not 0 for all  . Then for this
. Then for this  and
and 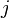 we have
we have 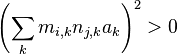 . This completes the proof.
. This completes the proof.
References
- ↑ "Bemerkungen zur Theorie der beschränkten Bilinearformen mit unendlich vielen Veränderlichen". Journal für die reine und angewandte Mathematik (Crelle's Journal) 1911 (140): 1–00. 1911. doi:10.1515/crll.1911.140.1.
- ↑ Zhang, Fuzhen, ed. (2005). "The Schur Complement and Its Applications". Numerical Methods and Algorithms 4. doi:10.1007/b105056. ISBN 0-387-24271-6., page 9, Ch. 0.6 Publication under J. Schur
- ↑ Ledermann, W. (1983). "Issai Schur and His School in Berlin". Bulletin of the London Mathematical Society 15 (2): 97–106. doi:10.1112/blms/15.2.97.