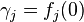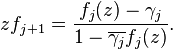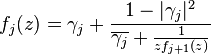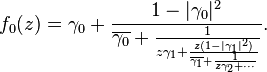Schur class

In mathematics, the Schur class consists of the Schur functions: the holomorphic functions from the open unit disk to the closed unit disk. These functions were studied by Schur (1918).

The Schur parameters γ_j of a Schur function f₀ are defined recursively by

\gamma_j=f_j(0)

zf_{j+1}=\frac{f_j(z)-\gamma_j}{1-\overline{\gamma_j}f_j(z)}.

The Schur parameters γ_j all have absolute value at most 1.

This gives a continued fraction expansion of the Schur function f₀ by repeatedly using the fact that

f_j(z)=\gamma_j+\frac{1-|\gamma_j|^2}{\overline {\gamma_j}+\frac{1}{zf_{j+1}(z)}}

which gives

f_0(z)=\gamma_0+\frac{1-|\gamma_0|^2}{\overline {\gamma_0}+\frac{1}{z \gamma_1+\frac{z(1-|\gamma_1|^2)}{\overline {\gamma_1}+\frac{1}{z\gamma_2+\cdots}}}}.

References

Schur, I. (1918), "Über Potenzreihen, die im Innern des Einheitskreises beschränkt sind. I, II", J. Reine Angew. Math. (in German) (Berlin: Walter de Gruyter) 147,: 205–232, doi:10.1515/crll.1917.147.205, Zbl 46.0475.01
Simon, Barry (2005), Orthogonal polynomials on the unit circle. Part 1. Classical theory, American Mathematical Society Colloquium Publications 54, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-3446-6, MR 2105088
Simon, Barry (2005), Orthogonal polynomials on the unit circle. Part 2. Spectral theory, American Mathematical Society Colloquium Publications 54, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-3675-0, MR 2105089