Schur-convex function

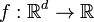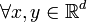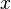In mathematics, a Schur-convex function, also known as S-convex, isotonic function and order-preserving function is a function $f: \mathbb{R}^d\rightarrow \mathbb{R}$ , for which if $\forall x,y\in \mathbb{R}^d$ where $x$ is majorized by 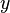$y$ , then 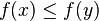$f(x)\le f(y)$ . Named after Issai Schur, Schur-convex functions are used in the study of majorization. Every function that is convex and symmetric is also Schur-convex. The opposite implication is not true, but all Schur-convex functions are symmetric (under permutations of the arguments).

Schur-concave function

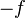A function $f$ is 'Schur-concave' if its negative, $-f$ , is Schur-convex.

A simple criterion

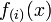If $f$ is Schur-convex and all first partial derivatives exist, then the following holds, where $f_{(i)}(x)$ denotes the partial derivative with respect to $x_i$ :

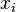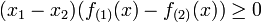(x_1 - x_2)(f_{(1)}(x) - f_{(2)}(x)) \ge 0

for all

x

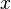. Since

f

is a symmetric function, the above condition implies all the similar conditions for the remaining indexes!

Examples

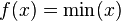$f(x)=\min(x)$ is Schur-concave while 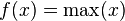$f(x)=\max(x)$ is Schur-convex. This can be seen directly from the definition.

The Shannon entropy function 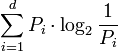$\sum_{i=1}^d{P_i \cdot \log_2{\frac{1}{P_i}}}$ is Schur-concave.

The Rényi entropy function is also Schur-concave.

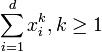$\sum_{i=1}^d{x_i^k},k \ge 1$ is Schur-convex.

The function 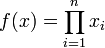$f(x) = \prod_{i=1}^n x_i$ is Schur-concave, when we assume all 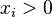$x_i > 0$ . In the same way, all the Elementary symmetric functions are Schur-concave, when $x_i > 0$ .

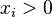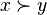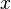A natural interpretation of majorization is that if $x \succ y$ then $x$ is more spread out than 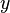$y$ . So it is natural to ask if statistical measures of variability are Schur-convex. The variance and standard deviation are Schur-convex functions, while the Median absolute deviation is not.

If 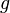$g$ is a convex function defined on a real interval, then 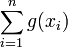$\sum_{i=1}^n g(x_i)$ is Schur-convex.

A probability example: If 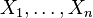$X_1, \dots, X_n$ are exchangeable random variables, then the function 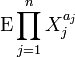$\text{E} \prod_{j=1}^n X_j^{a_j}$ is Schur-convex as a function of $a=(a_1, \dots, a_n)$ , assuming that the expectations exist.

The Gini coefficient is strictly Schur concave.

Schur-convex function

Schur-concave function

A simple criterion

Examples

See also