Schur's lemma (from Riemannian geometry)

Schur's lemma is a result in Riemannian geometry that says, heuristically, whenever certain curvatures are pointwise constant then they are forced to be globally constant. It is essentially a degree of freedom counting argument.

Statement of the Lemma

Suppose 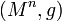$(M^n,g)^{}_{}$ is a Riemannian manifold and 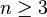$n \geq 3$ . Then if

the sectional curvature is pointwise constant, that is, there exists some function 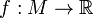$f:M \rightarrow \mathbb{R}$ such that

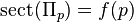\mathrm{sect}^{}_{}(\Pi_p) = f(p)

for all two-dimensional subspaces

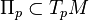\Pi_p \subset T_p M

and all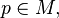

p \in M,

then

f

is constant, and the manifold has constant sectional curvature (also known as a space form when

M

is complete); alternatively

the Ricci curvature endomorphism is pointwise a multiple of the identity, that is, there exists some function 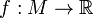$f:M \rightarrow \mathbb{R}$ such that

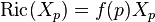\mathrm{Ric}^{}_{}(X_p) = f(p) X_p

for all

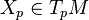X_p \in T_p M

and all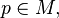

p \in M,

then

f

is constant, and the manifold is Einstein.

The requirement that 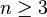$n \geq 3$ cannot be lifted. This result is far from true on two-dimensional surfaces. In two dimensions sectional curvature is always pointwise constant since there is only one two-dimensional subspace 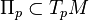$\Pi_p \subset T_p M$ , namely 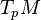$T_p M$ . Furthermore, in two dimensions the Ricci curvature endomorphism is always a multiple of the identity (scaled by Gauss curvature). On the other hand, certainly not all two-dimensional surfaces have constant sectional (or Ricci) curvature.

Reference

S. Kobayashi, K. Nomizu. Foundations of Differential Geometry (Wiley Classics Library) Volume 1, page 202.