Schur–Zassenhaus theorem
The Schur–Zassenhaus theorem is a theorem in group theory which states that if  is a finite group, and
is a finite group, and 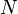 is a normal subgroup whose order is coprime to the order of the quotient group
is a normal subgroup whose order is coprime to the order of the quotient group 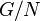 , then
, then  is a semidirect product (aka split[ting] extension) of
is a semidirect product (aka split[ting] extension) of 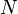 and
and 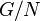 .
.
An alternative statement of the theorem is that any normal Hall subgroup 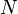 of a finite group
of a finite group  has a complement in
has a complement in  . In some textbooks (e.g. Isaac or Rose), the Schur–Zassenhaus theorem is stated with the additional conclusion that all complements of
. In some textbooks (e.g. Isaac or Rose), the Schur–Zassenhaus theorem is stated with the additional conclusion that all complements of 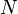 in G are conjugate. All known proofs of the conjugacy conclusion require the use of the (more recent) Feit-Thompson theorem.
in G are conjugate. All known proofs of the conjugacy conclusion require the use of the (more recent) Feit-Thompson theorem.
The Schur–Zassenhaus theorem at least partially answers the question: "In a composition series, how can we classify groups with a certain set of composition factors?" The other part, which is where the composition factors do not have coprime orders, is tackled in extension theory.
According to Rotman, Issai Schur (1904) proved the theorem for the special case when the complement of 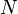 is cyclic and Hans Zassenhaus (1937) extended it for arbitrary complements. Kurzweil and Stellmacher cite a 1907 publication in of Schur in Crelle's Journal for his result. Humphreys cites a similarly titled 1904 paper of Schur (in the same journal) for the first results in central extensions, which are motivated by failure of the semidirect construction.
is cyclic and Hans Zassenhaus (1937) extended it for arbitrary complements. Kurzweil and Stellmacher cite a 1907 publication in of Schur in Crelle's Journal for his result. Humphreys cites a similarly titled 1904 paper of Schur (in the same journal) for the first results in central extensions, which are motivated by failure of the semidirect construction.
Examples and non-examples
It is clear that if we do not impose the coprime condition, the theorem is not true: consider for example the cyclic group 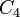 and its normal subgroup
and its normal subgroup 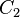 . Then if
. Then if 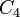 were a semidirect product of
were a semidirect product of 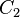 and
and 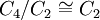 then
then 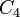 would have to contain two elements of order 2, but it only contains one. Another way to explain this impossibility of splitting
would have to contain two elements of order 2, but it only contains one. Another way to explain this impossibility of splitting 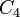 (i.e. expressing it as a semidirect product) is to observe that the automorphisms of
(i.e. expressing it as a semidirect product) is to observe that the automorphisms of 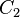 are the trivial group, so the only possible [semi]direct product of
are the trivial group, so the only possible [semi]direct product of 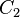 with itself is a direct product (which gives rise to the Klein four-group, a group that is non-isomorphic with
with itself is a direct product (which gives rise to the Klein four-group, a group that is non-isomorphic with 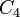 ).
).
An example where the Schur–Zassenhaus theorem does apply is the symmetric group on 3 symbols,  , which has a normal subgroup of order 3 (isomorphic with
, which has a normal subgroup of order 3 (isomorphic with 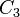 ) which in turn has index 2 in
) which in turn has index 2 in  (in agreement with the theorem of Lagrange), so
(in agreement with the theorem of Lagrange), so 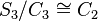 . Since 2 and 3 are relatively prime, the Schur–Zassenhaus theorem applies and
. Since 2 and 3 are relatively prime, the Schur–Zassenhaus theorem applies and 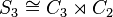 . Note that the automorphism group of
. Note that the automorphism group of 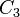 is
is 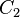 and the automorphism of
and the automorphism of 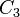 used in the semidirect product that gives rise to
used in the semidirect product that gives rise to  is the non-trivial automorphism that permutes the two non-identity elements of
is the non-trivial automorphism that permutes the two non-identity elements of 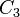 . Furthermore, the three subgroups of order 2 in
. Furthermore, the three subgroups of order 2 in  (any of which can serve as a complement to
(any of which can serve as a complement to 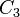 in
in  ) are conjugate to each other.
) are conjugate to each other.
The non-triviality of the (additional) conjugacy conclusion can be illustrated with the Klein four-group 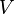 as the non-example. Any of the three proper subgroups of
as the non-example. Any of the three proper subgroups of 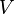 (all of which have order 2) is normal in
(all of which have order 2) is normal in 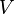 ; fixing one of these subgroups, any of the other two remaining (proper) subgroups complements it in
; fixing one of these subgroups, any of the other two remaining (proper) subgroups complements it in 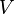 , but none of these three subgroups of
, but none of these three subgroups of 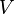 is a conjugate of any other one, because
is a conjugate of any other one, because 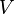 is Abelian.
is Abelian.
The converse of the Schur–Zassenhaus theorem does not hold, i.e. there are semidirect products where the coprimality of index and order doesn't hold. For example, the dihedral group of order 8 is isomorphic with 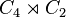 . It is also worth noting that there exists another group of order 8, the quaternion group that has normal subgroups of order 4 and 2 but is not a [semi]direct product. Schur's paper(s) at the beginning of the 20th century introduced the notion of central extension to address examples such as such
. It is also worth noting that there exists another group of order 8, the quaternion group that has normal subgroups of order 4 and 2 but is not a [semi]direct product. Schur's paper(s) at the beginning of the 20th century introduced the notion of central extension to address examples such as such 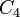 and the quaternions.
and the quaternions.
References
- Joseph J. Rotman (1995). An Introduction to the Theory of Groups. New York: Springer–Verlag. ISBN 978-0-387-94285-8.
- David S. Dummit & Richard M. Foote (2003). Abstract Algebra. Wiley. ISBN 978-0-471-43334-7.
- John S. Rose (1978). A Course on Group Theory. Cambridge University Press. ISBN 0-521-21409-2.
- I. Martin Isaacs (2008). Finite Group Theory. American Mathematical Society. ISBN 978-0-8218-4344-4.
- Hans Kurzweil & Bernd Stellmacher (2004). The Theory of Finite Groups: An Introduction. Springer-Verlag. ISBN 0-387-40510-0.
- James E. Humphreys (1996). A Course in Group Theory. Oxford University Press. ISBN 0-19-853459-0.
- J. Schur: Über die Darstellung der endlichen Gruppen durch gebrochen lineare Substitutionen. Journal für die reine und angewandte Mathematik 127 (1904): 20-50.
- J. Schur: Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen, J. reine u. angew. Math. 132 (1907), 85-137.
- H. Zassenhaus: Lehrbuch der Gruppentheorie. Leipzig 1937.