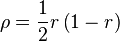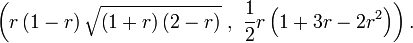Schoch line
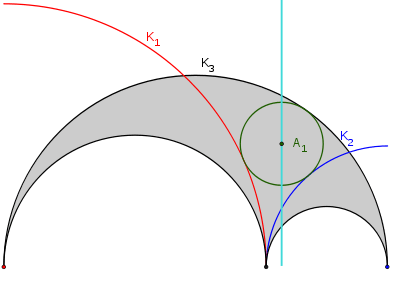
In geometry, the Schoch line is a line defined from an arbelos and named by Peter Woo after Thomas Schoch, who had studied it in conjunction with the Schoch circles.
Construction
An arbelos is a shape bounded by three mutually-tangent semicircular arcs with collinear endpoints, with the two smaller arcs nested inside the larger one; let the endpoints of these three arcs be (in order along the line containing them) A, B, and C. Let K1 and K2 be two more arcs, centered at A and C, respectively, with radii AB and CB, so that these two arcs are tangent at B; let K3 be the largest of the three arcs of the arbelos. A circle, with the center A1, is then created tangent to the arcs K1,K2, and K3. This circle is congruent with Archimedes' twin circles, making it an Archimedean circle; it is one of the Schoch circles. The Schoch line is perpendicular to the line AC and passes through the point A1. It is also the location of the centers of infinitely many Archimedean circles, e.g. the Woo circles.[1]
Radius and center of A1
If r = AB/AC, and AC = 1, then the radius of A1 is
and the center is
References
- ↑ 1.0 1.1 Dodge, Clayton W.; Schoch, Thomas; Woo, Peter Y.; Yiu, Paul (1999), "Those ubiquitous Archimedean circles", Mathematics Magazine 72 (3): 202–213, doi:10.2307/2690883, MR 1706441.
Additional reading
- Okumura, Hiroshi; Watanabe, Masayuki (2004), "The Archimedean circles of Schoch and Woo", Forum Geometricorum 4: 27–34, MR 2057752.
External links
- van Lamoen, Floor. "Schoch Line." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein". Retrieved 2008-04-11.