Schnorr signature
In cryptography, a Schnorr signature is a digital signature produced by the Schnorr signature algorithm. Its security is based on the intractability of certain discrete logarithm problems. The Schnorr signature is considered the simplest[1] digital signature scheme to be provably secure in a random oracle model.[2] It is efficient and generates short signatures. It is covered by U.S. Patent 4,995,082, which expired in February 2008.
Algorithm
Choosing parameters
- All users of the signature scheme agree on a group
 with generator
with generator 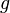 of prime order
of prime order 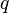 in which the discrete log problem is hard. Typically a Schnorr group is used.
in which the discrete log problem is hard. Typically a Schnorr group is used. - All users agree on a cryptographic hash function
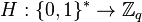 .
.
Notation
In the following,
- Exponentiation stands for repeated application of the group operation
- Juxtaposition stands for multiplication on the set of congruence classes or application of the group operation (as applicable)
- Subtraction stands for subtraction on set of equivalence groups
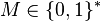 , the set of finite bit strings
, the set of finite bit strings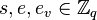 , the
, the 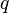
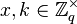 , the multiplicative group of integers modulo
, the multiplicative group of integers modulo 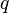 (for prime
(for prime 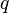 ,
, 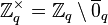 )
)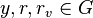 .
.
Key generation
- Choose a private signing key
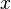 from the allowed set.
from the allowed set. - The public verification key is
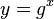 .
.
Signing
To sign a message 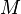 :
:
- Choose a random
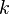 from the allowed set.
from the allowed set. - Let
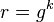 .
. - Let
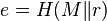 , where
, where 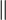 denotes concatenation and
denotes concatenation and  is represented as a bit string.
is represented as a bit string. - Let
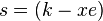 .
.
The signature is the pair 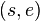 .
.
Note that 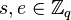 ; if
; if 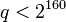 , then the signature representation can fit into 40 bytes.
, then the signature representation can fit into 40 bytes.
Verifying
- Let
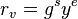
- Let
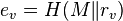
If 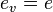 then the signature is verified.
then the signature is verified.
Proof of correctness
It is relatively easy to see that 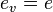 if the signed message equals the verified message:
if the signed message equals the verified message:
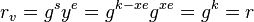 , and hence
, and hence 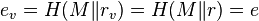 .
.
Public elements:  ,
, 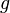 ,
, 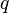 ,
, 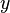 ,
,  ,
,  ,
,  .
Private elements:
.
Private elements: 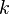 ,
, 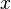 .
.
Security argument
The signature scheme was constructed by applying the Fiat–Shamir transform[3] to Schnorr's identification protocol.[4] Therefore (per Fiat and Shamir's arguments), it is secure if 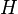 is modeled as a random oracle.
is modeled as a random oracle.
Its security can also be argued in the generic group model, under the assumption that 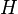 is "random-prefix preimage resistant" and "random-prefix second-preimage resistant".[5] In particular,
is "random-prefix preimage resistant" and "random-prefix second-preimage resistant".[5] In particular, 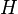 does not need to be collision resistant.
does not need to be collision resistant.
In 2012, Seurin[2] provided an exact proof of the Schnorr signature scheme. In particular, Seurin shows that the security proof using the Forking lemma is the best possible result for any signature schemes based on one-way group homomorphisms including Schnorr-Type signatures and the Guillou-Quasiquater signature schemes. Namely, under the ROMDL assumption, any algebraic reduction must lose a factor 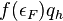 in its time-to-success ratio, where
in its time-to-success ratio, where 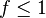 is a function that remains close to 1 as long as "
is a function that remains close to 1 as long as "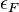 is noticeably smaller than 1", where
is noticeably smaller than 1", where 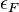 is the probability of forging an error making at most
is the probability of forging an error making at most 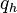 queries to the random oracle.
queries to the random oracle.
See also
References
- ↑ Savu, Laura (2012). "SIGNCRYPTION SCHEME BASED ON SCHNORR DIGITAL SIGNATURE". arXiv.org.
- ↑ 2.0 2.1 Seurin, Yannick (2012-01-12). "On the Exact Security of Schnorr-Type Signatures in the Random Oracle Model". Cryptology ePrint Archive. International Association for Cryptologic Research. Retrieved 2014-08-11.
- ↑ Fiat; Shamir (1986). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Proceedings of CRYPTO '86.
- ↑ Schnorr (1989). "Efficient Identification and Signatures for Smart Cards". Proceedings of CRYPTO '89.
- ↑ Neven, Smart, Warinschi. "Hash Function Requirements for Schnorr Signatures". IBM Research. Retrieved 19 July 2012.
- C.P. Schnorr, Efficient identification and signatures for smart cards, in G. Brassard, ed. Advances in Cryptology—Crypto '89, 239-252, Springer-Verlag, 1990. Lecture Notes in Computer Science, nr 435
- Claus-Peter Schnorr, Efficient Signature Generation by Smart Cards, J. Cryptology 4(3), pp161–174 (1991) (PS).
- Menezes, Alfred J. et al. Handbook of Applied Cryptography CRC Press. 1996.
| ||||||||||||||||||||||||||||||||||||