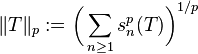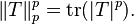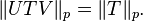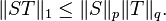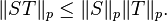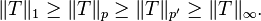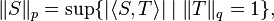Schatten norm
In mathematics, specifically functional analysis, the Schatten norm (or Schatten–von-Neumann norm) arises as a generalization of p-integrability similar to the trace class norm and the Hilbert–Schmidt norm.
Definition
Let 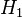 ,
, 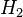 be separable Hilbert spaces, and
be separable Hilbert spaces, and  a (linear) bounded operator from
a (linear) bounded operator from
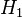 to
to 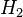 . For
. For 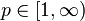 , define the Schatten p-norm of
, define the Schatten p-norm of  as
as
for 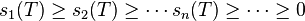 the singular values of
the singular values of  , i.e. the eigenvalues of the Hermitian matrix
, i.e. the eigenvalues of the Hermitian matrix 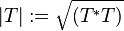 .
From functional calculus on the positive operator T * T it follows that
.
From functional calculus on the positive operator T * T it follows that
Properties
In the following we formally extend the range of  to
to ![[1,\infty]](../I/m/a61549fc881cace1ae16a7307ab8ee9d.png) . The dual index to
. The dual index to  is then
is then 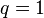 .
.
- The Schatten norms are isometrically invariant: for isometries
 and
and  and
and ![p\in [1,\infty]](../I/m/c4c80a6c10fc00791efca5fe92c6ee51.png) ,
,
- They satisfy Hölder's inequality: for all
![p\in [1,\infty]](../I/m/c4c80a6c10fc00791efca5fe92c6ee51.png) and
and  such that
such that 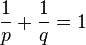 , and operators
, and operators 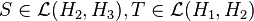 defined between Hilbert spaces
defined between Hilbert spaces 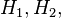 and
and 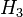 respectively,
respectively,
- Sub-multiplicativity: For all
![p\in [1,\infty]](../I/m/c4c80a6c10fc00791efca5fe92c6ee51.png) and operators
and operators 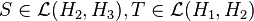 defined between Hilbert spaces
defined between Hilbert spaces 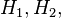 and
and 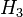 respectively,
respectively,
- Monotonicity: For
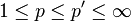 ,
,
- Duality: Let
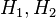 be finite-dimensional Hilbert spaces,
be finite-dimensional Hilbert spaces, ![p\in [1,\infty]](../I/m/c4c80a6c10fc00791efca5fe92c6ee51.png) and
and  such that
such that 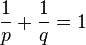 , then
, then
where 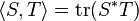 denotes the Hilbert-Schmidt inner product.
denotes the Hilbert-Schmidt inner product.
Remarks
Notice that 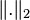 is the Hilbert–Schmidt norm (see Hilbert–Schmidt operator) and
is the Hilbert–Schmidt norm (see Hilbert–Schmidt operator) and 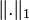 is the trace class norm (see trace class).
is the trace class norm (see trace class).
For 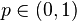 the function
the function 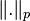 is an example of a quasinorm.
is an example of a quasinorm.
An operator which has a finite Schatten norm is called a Schatten class operator and the space of such operators is denoted by 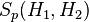 . With this norm,
. With this norm, 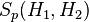 is a Banach space, and a Hilbert space for p = 2.
is a Banach space, and a Hilbert space for p = 2.
Observe that 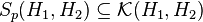 , the algebra of compact operators. This follows from the fact that if the sum is finite the spectrum will be finite or countable with the origin as limit point, and hence a compact operator (see compact operator on Hilbert space).
, the algebra of compact operators. This follows from the fact that if the sum is finite the spectrum will be finite or countable with the origin as limit point, and hence a compact operator (see compact operator on Hilbert space).
References
- Rajendra Bhatia, Matrix analysis, Vol. 169. Springer Science & Business Media, 1997.
- John Watrous, Theory of Quantum Information, 2.3 Norms of operators, lecture notes, University of Waterloo, 2011.
- Joachim Weidmann, Linear operators in Hilbert spaces, Vol. 20. Springer, New York, 1980.